Lecture 28: Outtro#
STATS 60 / STATS 160 / PSYCH 10
Concepts and Learning Goals:
Overview of what you learned this quarter!
tl;dr: three themes
What’s next if you’re stats-curious?
Remembering our journey#
Unit 1: Thinking about scale#
In statistics and data science, we are trying to use numbers to
Describe our observations
Quantify how confident we are
Numbers are only meaningful in context.
Is $ 10 billion a lot of money?
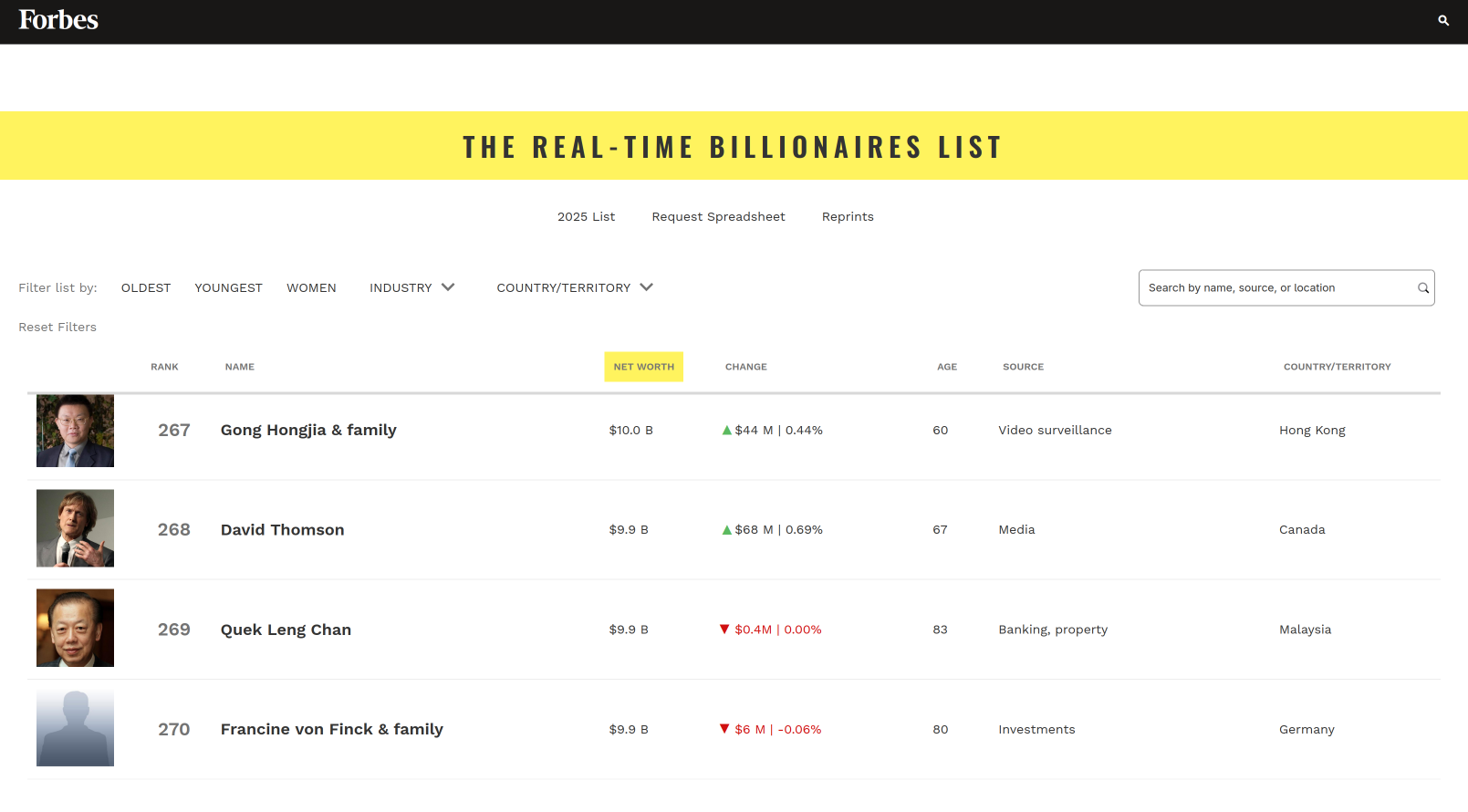
Forbes' real-time billionaires' list
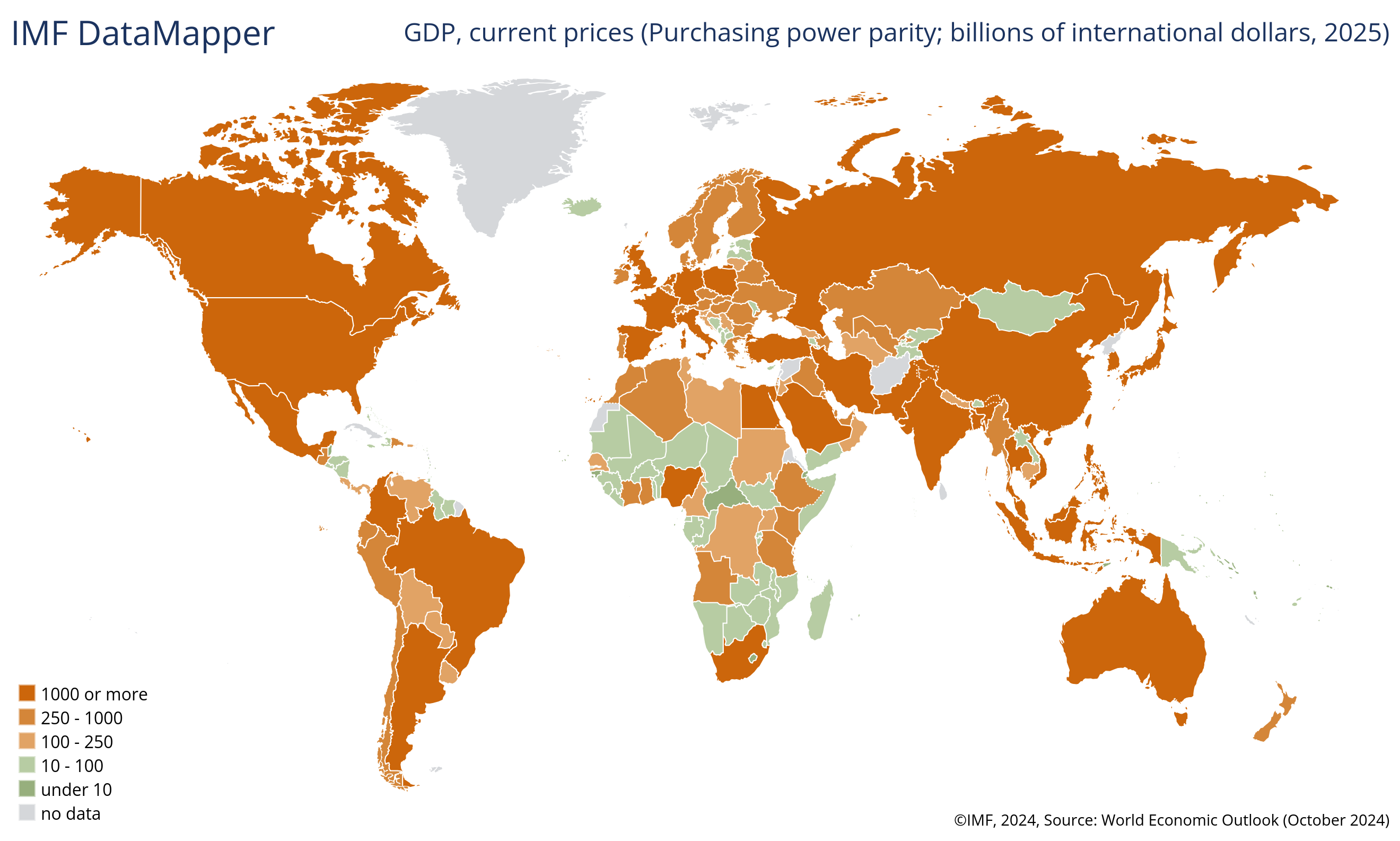
GDP heat map, in billions
Unit 1 was about building tools for contextualizing numbers and thinking critically about scale:
Three questions for contextualizing numbers:
What type of number is this?
What can I compare this number to? Is it large or small compared to other similar values?
What would I have expected this number to be?
Ballpark estimates for estimating a number
Set up a simple model to compute the quantity approximately by break up the estimate into small parts
How many visitors go on guided tours at Stanford per year?
(# visitors / year) = (# days/ year) x (# tours/ day) x (# visitors / tour)
Approximate parts up to a factor of 10
Cost-benefit analysis: a simple model helps us make difficult decisions
Unit 2: Probability#
A mathematical framework for modeling uncertain scenarios.
Is an observed pattern meaningful, or just random noise?
The probability we learned was essential for:
Hypothesis testing
Confidence intervals for estimation
Understanding selection bias
Topics covered:
Probabilistic experiments
Formalism: sample spaces, outcomes, events, probabilities
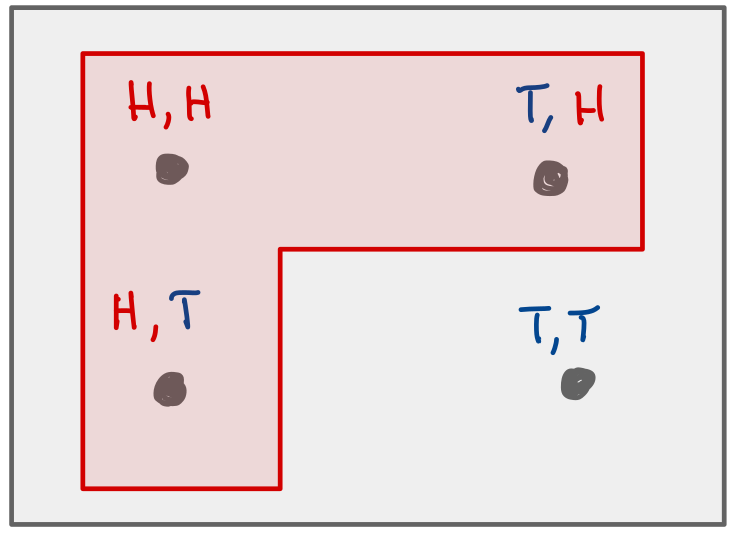
Modeling almost everything with coinflips, dice, and bags of marbles
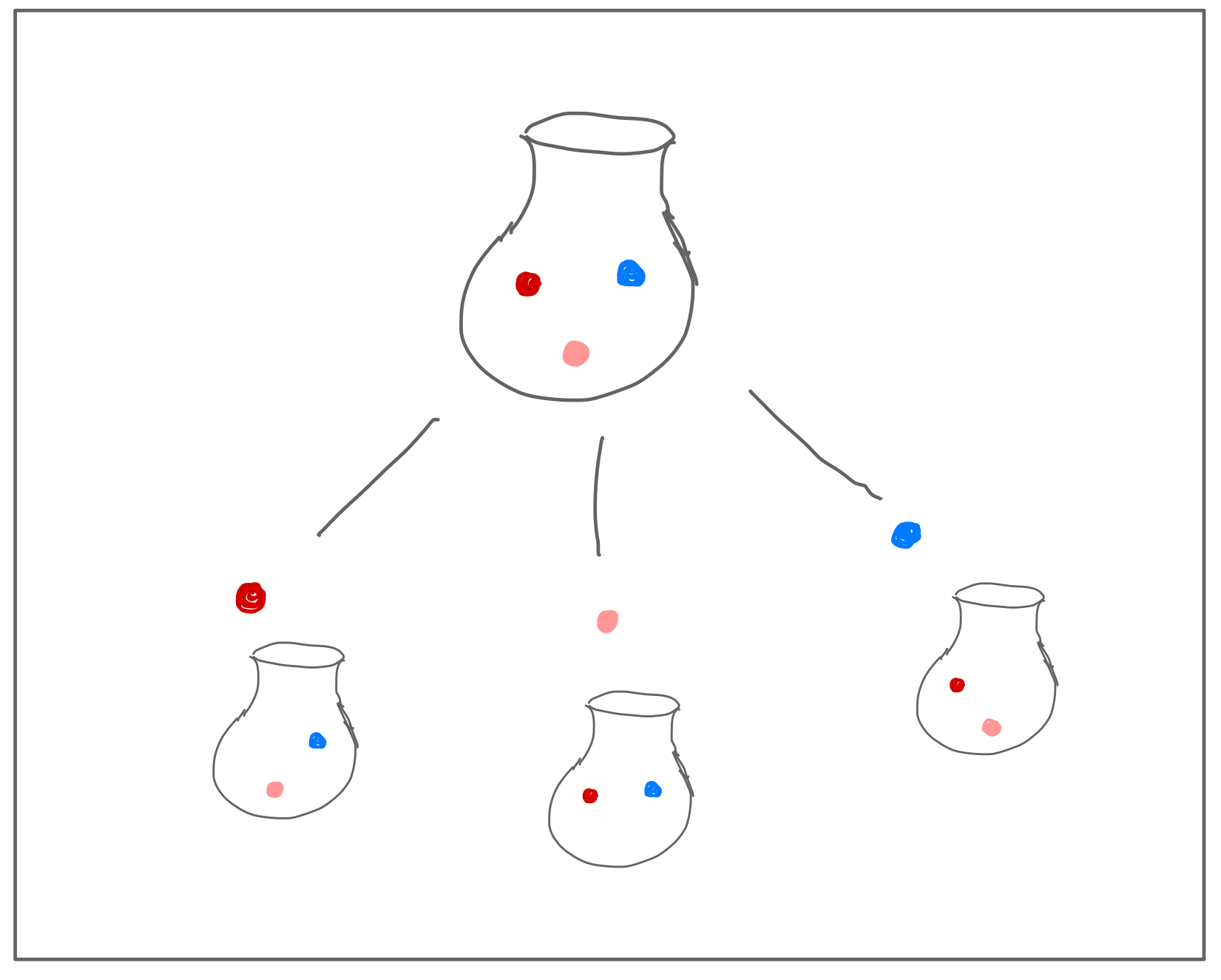
Drawing a marble from the bag.
Coincidences?
Even if an event is rare, it is likely to happen when you repeat an experiment many times
Example: the birthday paradox
Example: winning streak
Example from unit 4: multiple testing!
Computing probabilities
Coinflips and binomial coefficients
Later used in computing \(p\)-values
Law of the complement
Conditional probability
“Zooming in”
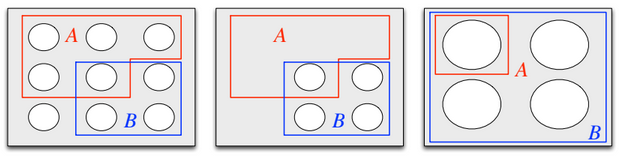
Zooming in on $B$. Image credit to Blitzstein and Hwang, chapter 2.
Bayes’ rule
Common mistakes in conditional probability:
Base rate fallacy: the conditional probability is not informative by itself (male-dominated sports)
\(\Pr[A \mid B] \neq \Pr[B \mid A]\) (distracted driving, gateway drugs)
Failing to condition on important information (OJ Simpson)
Generalizing from a biased sample or failing to realize you have conditioned (hot guys are jerks, selection bias)
Unit 3: Exploratory Data Analysis#
The entire dataset is TMI. How can we extract useful information?
Topics Covered:
Data visualization
Common graphic representations: pie chart, bar chart, time series, histogram, scatterplot
Best practices
Misleading and uninformative charts

Summaries of center: what is the one number that best summarizes the data?
mean, median
Variability: how similar are the different datapoints in the dataset?
Would you rather be given \(\$150\) or flip a coin for \(\$300\)?
Variance and standard deviation
Quantiles and gaps between quantiles
Correlation and correlation coefficient
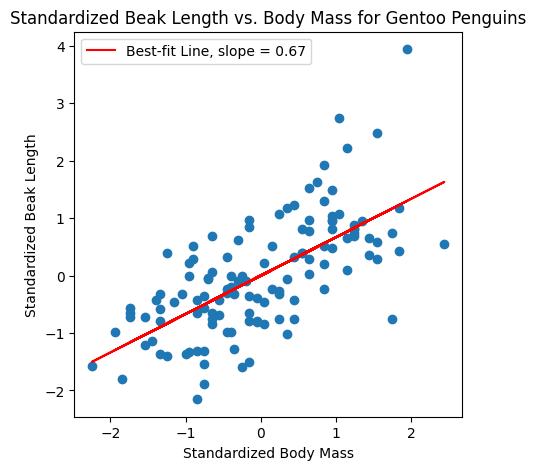
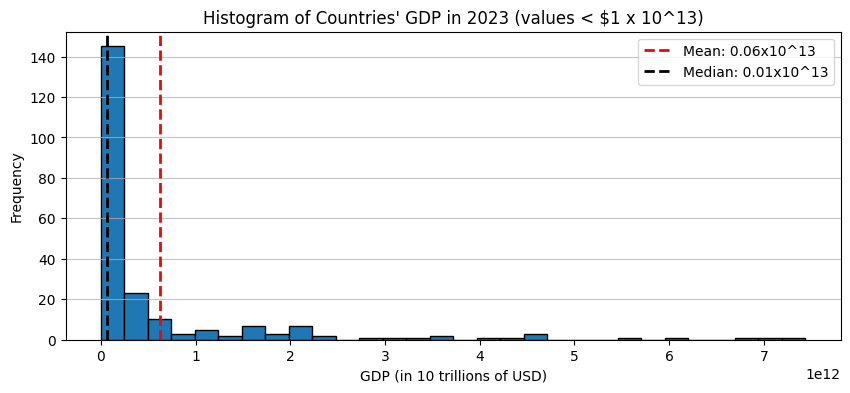
The usefulness of a summary statistic depends on the data!
outliers
skew
multi-modal data
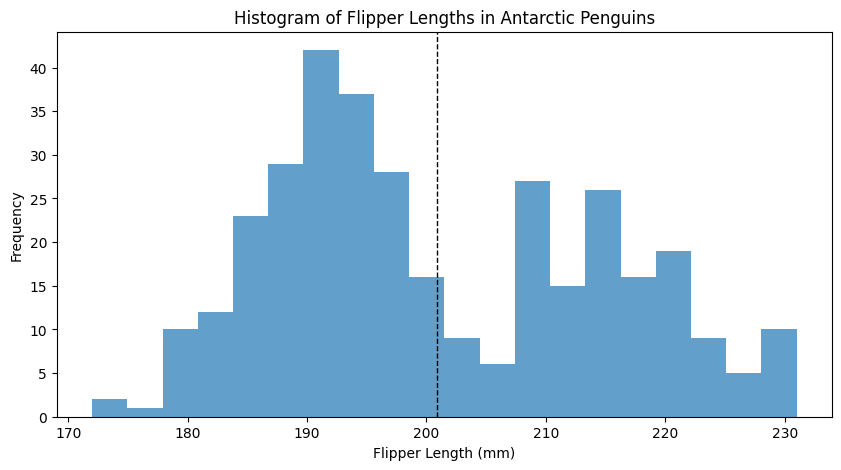
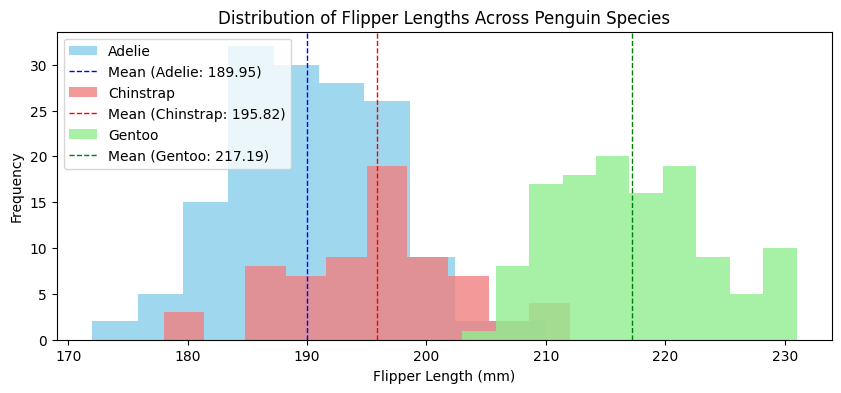
Unit 4: Correlation and Experiments#
How to analyze data for trends, and how to design experiments.
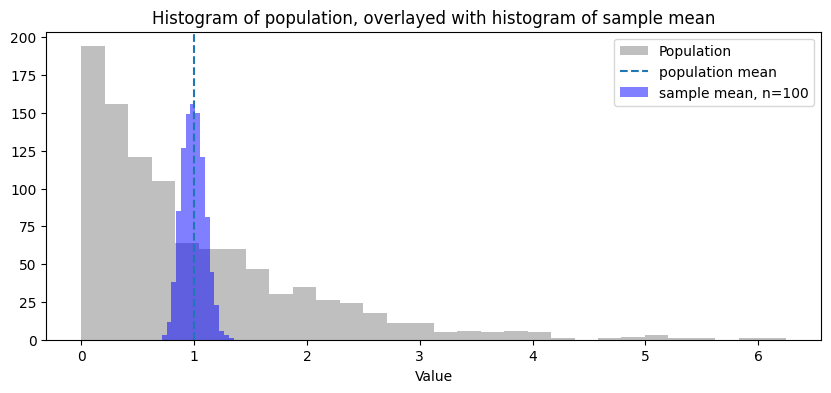
Effect of sample size on estimates
Sample vs. population
Sample size matters for estimation!
The standard deviation of the sample mean is \(\frac{\sigma}{\sqrt{n}}\)
To get \(10\) times more accurate, you need \(100\) times more samples.
Normal Approximation for the sample mean
Confidence intervals
68-95-99 rule

Selection bias dramatically affects estimates!
Gettysburg address experiment
Common sources of selection bias
Hypothesis testing: is my observation a real trend, or just noise?
Null hypothesis: a probability model for “just noise”
\(p\)-value: the chance we observed our outcome, or something more extreme, under the null hypothesis
Significance level, false positive rate, and multiple testing
Using simulation to compute \(p\)-values:
Testing for correlation
Potential outcomes model
Randomized controlled experiments
Drawbacks of observational studies
Correlation vs. causation and confounding/hidden variables
Effect of selection bias
Potential outcomes model
Unit 5: Machine Learning and Regression#
Statistics is often concerned with making predictions.
On observation \(x\), predict outcome \(y\).
\(x\) is symptoms/test results, \(y\) is diagnosis
\(x\) is SAT score, \(y\) is first-year GPA
\(x\) is weather now, \(y\) is weather later
We construct a simple model \(f\) so that \(f(x) = \hat{y}\), with the goal that \(\hat{y}\) is as close to \(y\) as possible.
Building models
It is easier to learn from examples than build a model by hand
“training” data
How to evaluate models: “training” vs. “testing”
Types of prediction problems:
regression
classification
text generation (next word prediction)
Examples of models
Linear and quadratic regression
\(k\)-nearest-neighbors
Markov text generators
Training data is everything!
Selection bias in training data leads to biased models
If \(x\) is far from all training examples, \(f(x)\) is probably not that accurate
More (good) data and better coverage improves performance
tl;dr: three themes#
The three major ideas that I want you to take away from this class.
Theme 1: Insight from simple models#
The world is complicated.
Answering a question exactly is overwelming and often impossible.
Strategy: construct a simple model of the situation.
At least within the simple model, we have the power to answer questions precisely and often quantitatively.
Ballpark estimates and cost-benefit analysis.
Hypothesis testing.
Machine learning and prediction.
Decision making in sports
With great power comes great responsibility.
Know the strengths and limitations of your model.
Theme 2: Conditioning matters#
We might understand an uncertain situation well, but everything can change if we condition!
Common mistakes in conditional probability
False positives for medical tests, distracted driving, OJ Simpson, male-dominated sports
Selection bias
Hot guys are jerks
Biased estimates
Biased ML predictions from biased training data
Multimodal data affects interpretation of summary statistics
Male vs. female penguin body mass
Does generic medical advice apply to you?
Salt, hypertension, men vs. women
Theme 3: Critical thinking is essential#
Once you specify the model, statistics can give precise answers.
Is our model good? Does it fit the situation?
Think critically! Don’t calculate blindly.
“When means mislead”
Usefulness of fundamental summary statistics (mean, median, standard deviation) depends on data (outliers, skew)
Correlation vs. causation
Confounding variables
Experimental design
Misleading graphs and figures
Multiple testing and \(p\)-hacking
We did a lot of “what does this mean in plain English?” exercises.
Thinking like this is important—I do this in my research and in my daily life constantly.
Even though a concept is formal and/or technical, we can and should try to really understand.
Feedback#
I want to make STATS60 great!
Please take a couple of minutes to give some feedback on the course this quarter.
I’m stats-curious. What’s next?#
If you like exploratory data analysis#
STATS 32: Introduction to R
Learn the basics of programming in R
Example/application-focused class
DATASCI 112: Principles of Data Science
Deeper dive into data visualization and data analysis
More machine learning: how to train and evaluate ML models
Practice programming basics
If you like experiments and hypothesis testing#
STATS 191: Introduction to Applied Statistics
Deeper dive into methods for data analysis and prediction
Applications to biology and social sciences
After taking probability theory,
STATS 200: Introduction to Theoretical Statistics
Hypothesis testing
Estimation and confidence intervals
Bayesian methods
Some theory of machine learning
If you like probability#
STATS 117: Introduction to probability theory
Dive into probability theory
Simple discrete models (coinflips, bags of marbles)
Continuous models (Normal)
STATS 118: Probablity theory for statistical inference
Deeper dive into probability theory
Theory behind the Normal approximation
Math behind some popular hypothesis tests
If you like machine learning#
CS 106EA: Exploring artifical intelligence
Training and evaluating ML models
How do neural networks work?
Challenges in ML: overfitting, bias, distribution shift
After taking MATH 51 and CS 106:
CS 129: Applied Machine Learning
More ML models:
logistic regression
support vector machines
deep learning
“Unsupervised learning”: clustering and feature discovery
