Lecture 4: Intro to probability#
STATS60, Stanford University Spring 2025
Announcements:
Office hours are now posted!
Please rebalance your sections. Michael’s section only has 2 attending.
This week: practice quizzes and reading (Blitzstein & Hwang, chapter 1) highly recommended.
Modeling uncertainty#
Probability is a branch of math designed for modeling uncertainty.
The main goals of statistics are:
Draw conclusions from data
Extract patterns from data
Make predictions based on data
But how do we know if what we observe is pattern, or coincidence?
Out of a survey of 100 random people, 55 prefer product A to product B.
Does the majority of the population prefer A?
A mid N.B.A. team suddenly wins 5 games in a row.
Is the streak likely to continue?
Many Cirrhosis patients at SF General hospital also experience migraine headaches.
Is a migraine headache a symptom of Cirrhosis?
Probability gives us a logical framework for deciding whether a pattern is “real” or “just a coincidence,” and for making predictions under uncertainty.
Test your intuition#
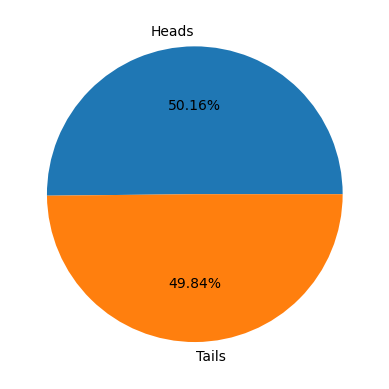
Suppose I flip a fair coin, and it comes up heads.
If I flip it a second time, is it more likely to come up heads or tails?
In \(10^6\) simulations:
import random
import matplotlib.pyplot as plt
num_H1 = 0
num_H1_H2 = 0
for t in range(1000000):
H1 = random.randint(0,1) # flip coin 1
H2 = random.randint(0,1) # flip coin 2
num_H1 += H1
if H1 == 1 and H2 == 1: # if both coins heads,
num_H1_H2 += 1 # increase tally
fig, ax = plt.subplots()
ax.pie([num_H1_H2, num_H1-num_H1_H2], labels=["Heads","Tails"], autopct='%1.2f%%')
plt.show()
Test your intuition, 2#
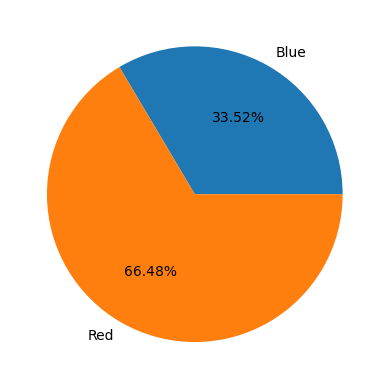
Suppose I have a bag with 2 red marbles and 2 blue marbles.
I draw a marble from the bag, and it is blue. I don’t return the marble to the bag.
If I draw another marble uniformly from the bag, is it more likely to be red or blue?
In \(10^6\) simulations:
num_B1 = 0
num_B1_B2 = 0
for t in range(1000000):
marbles = [1,2,3,4] # red are odd, blue are even
M1 = random.choice(marbles)
marbles.remove(M1)
M2 = random.choice(marbles)
if M1 == 2 or M1 == 4: # count if first marble blue (even)
num_B1 += 1
if M2 == 2 or M2 == 4: # and if second is blue (even)
num_B1_B2 += 1
fig, ax = plt.subplots()
ax.pie([num_B1_B2, num_B1-num_B1_B2], labels=["Blue","Red"], autopct='%1.2f%%')
plt.show()
Experiments and Outcomes#
An experiment is the (random) selection of an outcome from a set of possible outcomes, called the sample space.

Outcomes in a sample space.
Each[1] outcome has a probability, which is the chance that you get that outcome from the experiment.
Coin toss#
Example: if I flip a fair coin, the two possible outcomes are “H” and “T.” Each has probability \(\frac{1}{2}\).
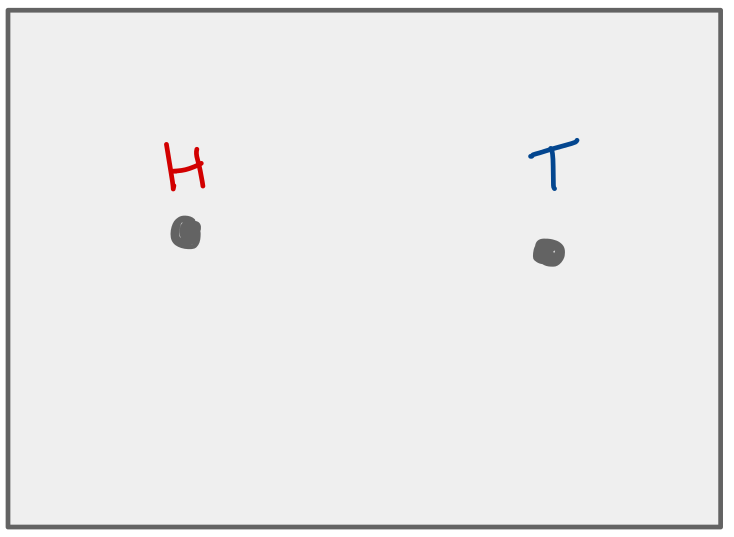
Coinflip.
Example: if I flip a fair coin twice, the four possible outcomes are “H,H”, “H,T”, “T,H”, and “T,T.” Each has probability \(\frac{1}{4}\).
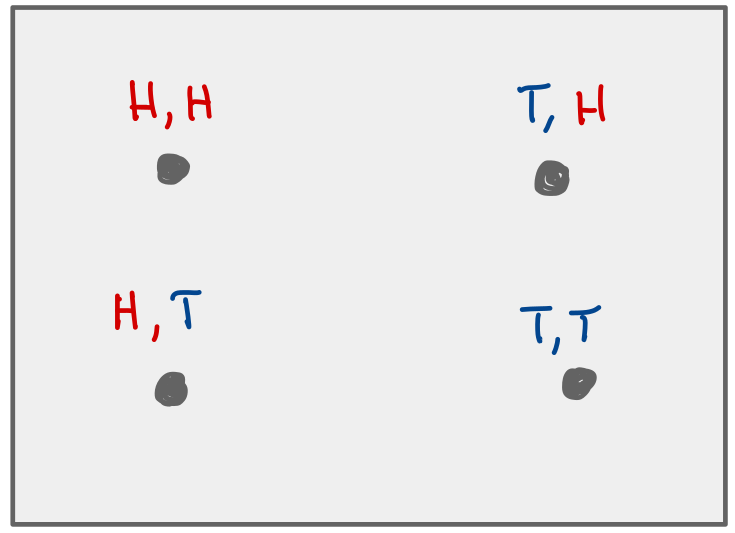
Two coin flips.
Events#
An event is a subset of the possible outcomes.
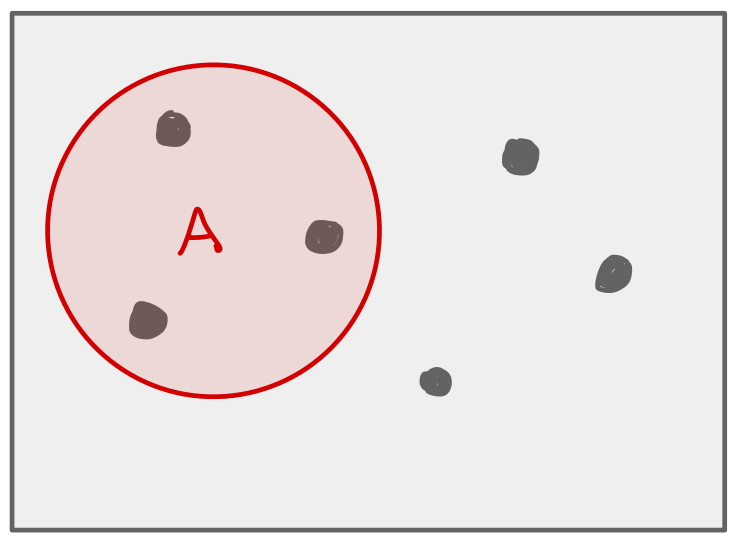
The event A.
Coin toss#
Example: The event that the first coin toss is “H”.
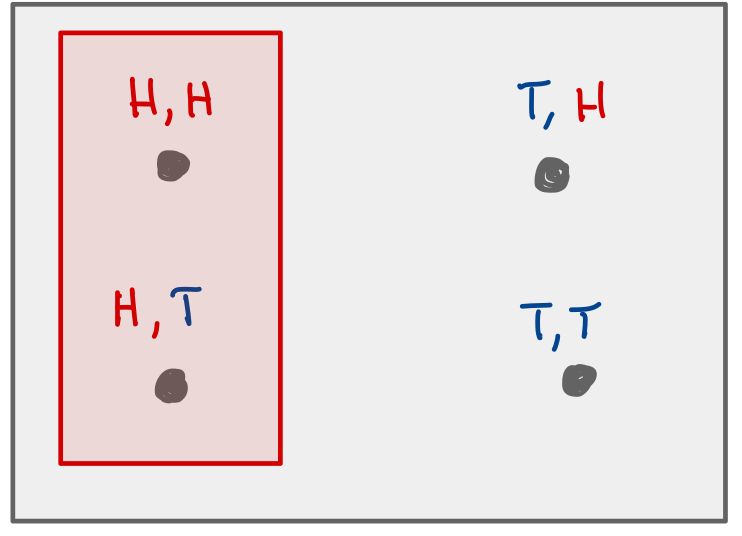
First is heads.
Example: The event that I toss at least one “H”.
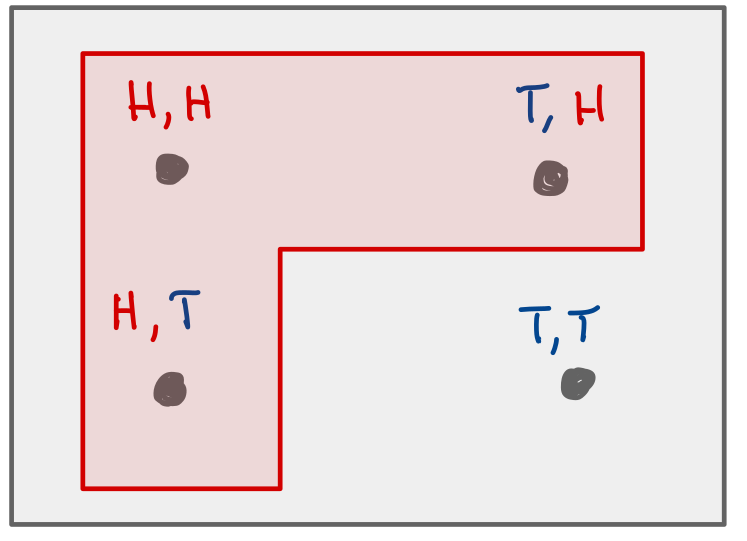
At least one heads.
Example: The event that both coin tosses are “H”.
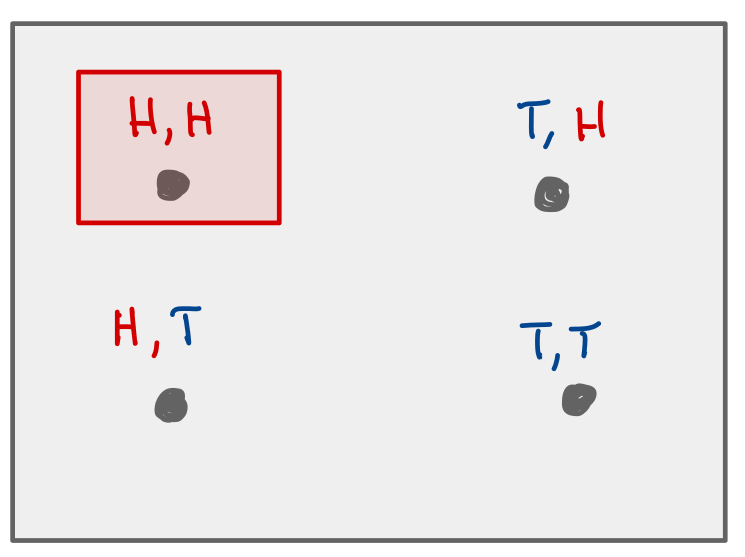
Both heads.
Test your understanding: What is the difference between an event and an outcome?
Operations on events#
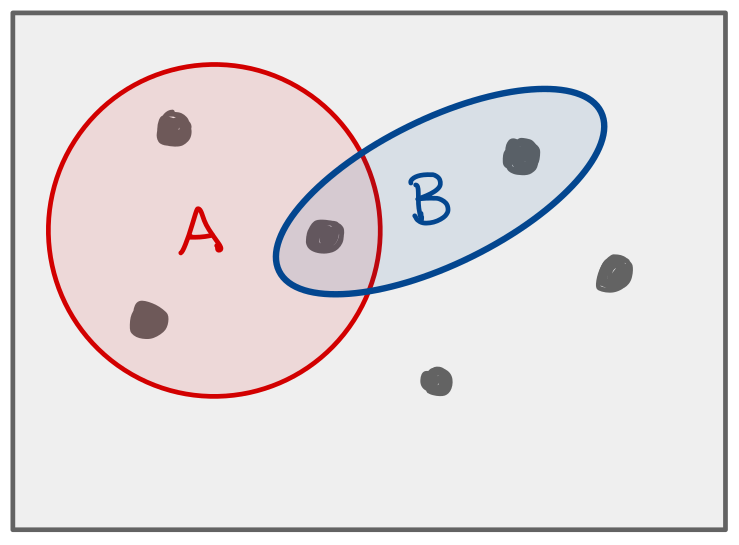
Events A and B.
We write \(\overline{A}\) or \(A^c\) to be the complement of \(A\).
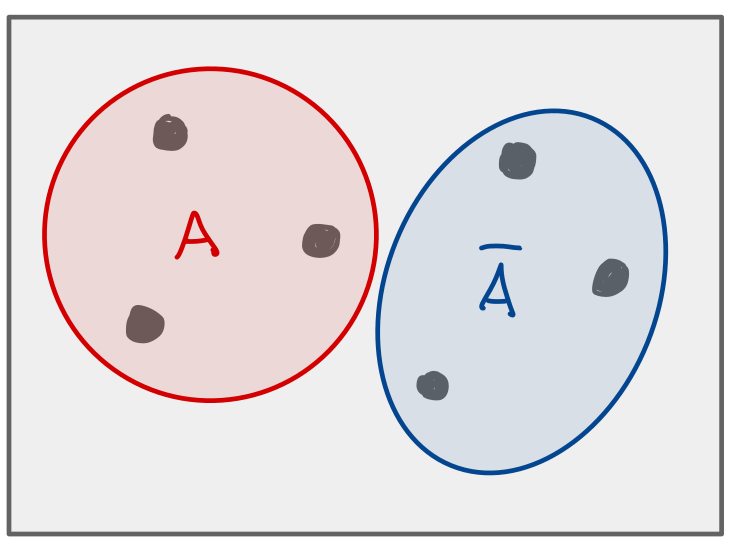
A complement.
For events \(A,B\), we write \(A \cup B\) to be the set of outcomes in either \(A\) or in \(B\). We say “A union B”.
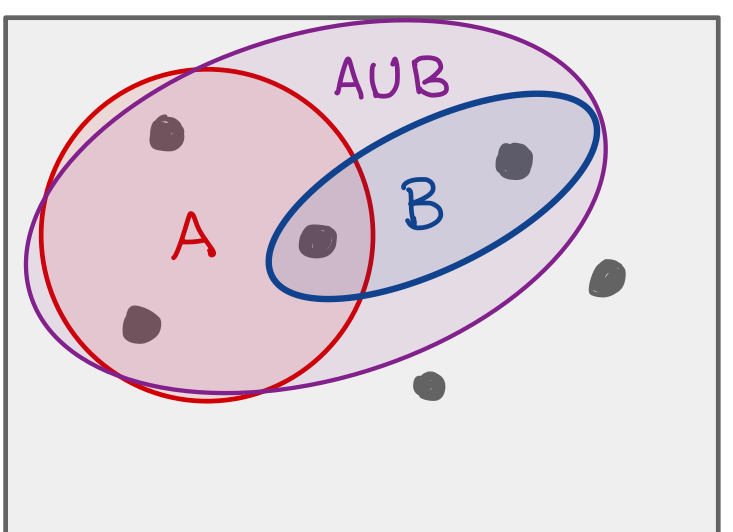
A union B.
We write \(A \cap B\) to be the set of outcomes in both \(A\) and \(B\). We say “A intersect B.”
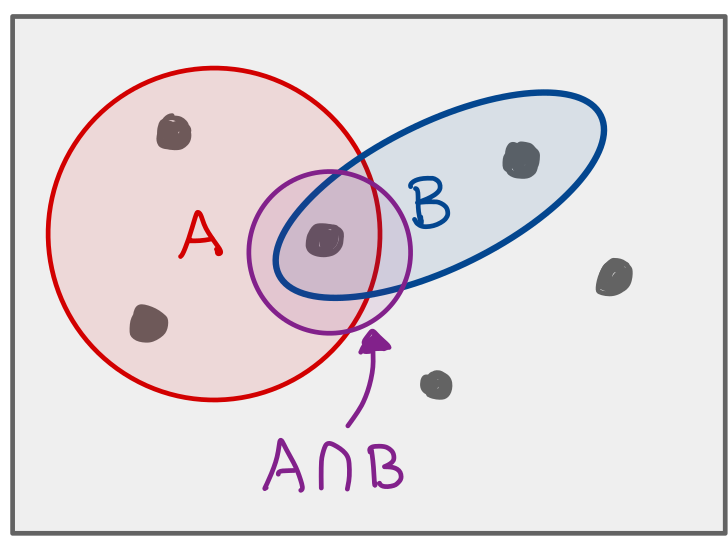
A intersect B.
Probability of an event#
If all outcomes of the experiment are equally likely, the probability of an event is just
This is the chance that the event occurs in the experiment.
If some outcomes are more likely than others, the probability of an event is a sum of the probabilities of all the outcomes in the event: $\( \Pr[A] = \sum_{a \in A} \Pr[a] \)$
Coin toss#
Example: What is the probability of the event that the first coin toss is “H”?

Example: What is the probability of the event that I toss at least one “H”?

Example: What is the probability of the event that both coin tosses are “H”?

Outcomes with unequal probability#
Example: the marbles#
What is the sample space for the following marbles scenario?
I have a bag with two red marbles and one blue marble.
This is the same as the experiment that occurs in our “marbles” example from before, when we remove a red marble from the bag first.
I draw a marble randomly from the bag.
What is the sample space?
Are the outcomes equally likely?
What is the probability of the event that the marble is blue?
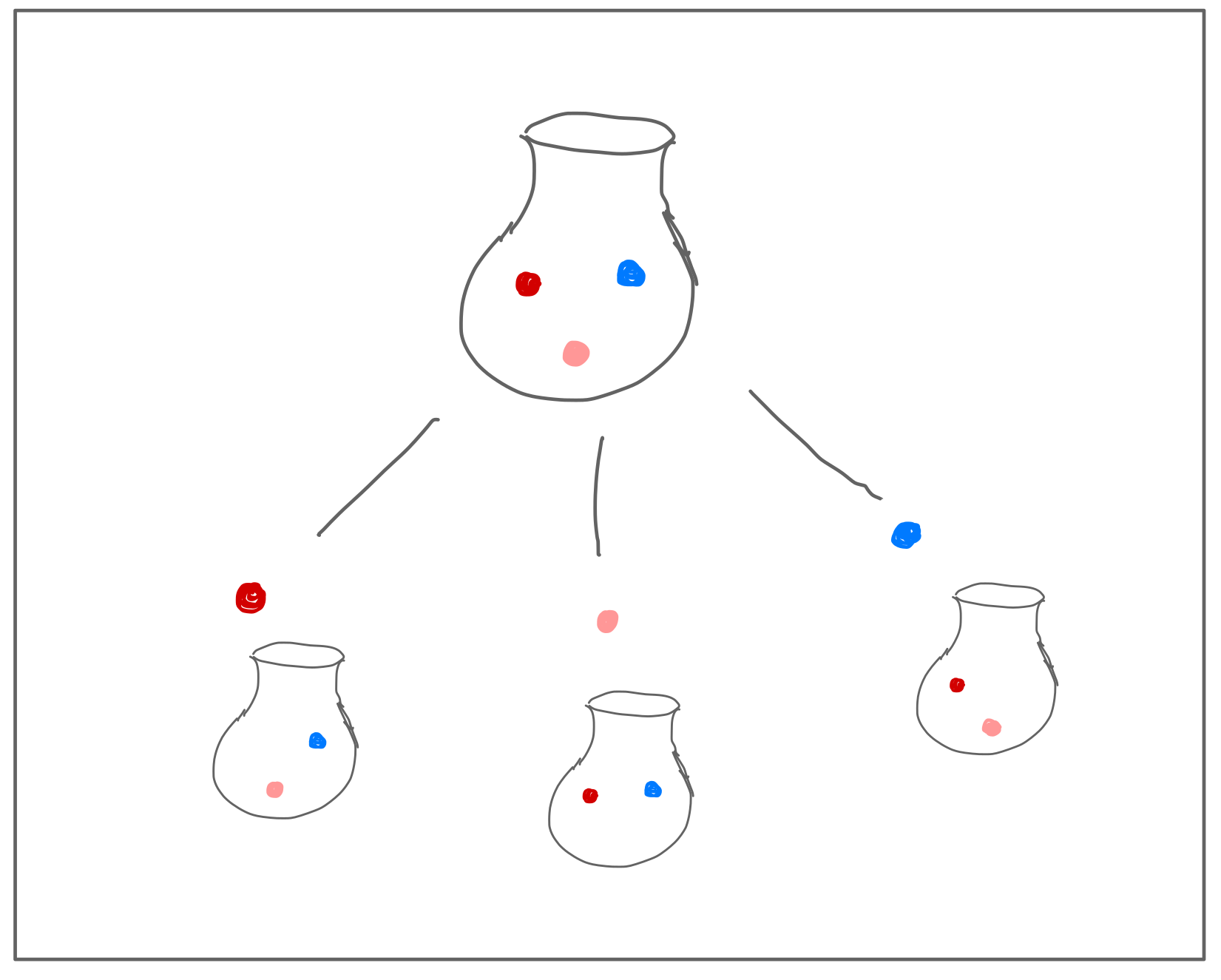
Drawing a marble from the bag.
Silly Leibniz#
A common mistake when computing probabilities is to treat outcomes as equally likely, even if they are not.
True or False: If I roll two six-sided dice, they are equally likely to sum to 11 as they are to sum to 12.
What are the outcomes in the event \(A\) that the sum is 11? What are the outcomes in the event \(B\) that the sum is 12?
There are two ways to look at it.
The first way: our experiment is we roll two dice, and report the outcomes in an unordered fashion. Here, there is only one outcome in each event: \(A\) has the single outcome \(\{5,6\}\) and \(B\) has the single outcome \(\{6,6\}\).
The second way: our experiment is that we roll two dice, and report the outcomes in order (or if you like, we roll one red and one blue dice). \(A\) has the outcomes \((5,6)\) and \((6,5)\), whereas \(B\) only has the outcome \((6,6)\).
Are the outcomes equally likely?
It depends on which way we define our experiment.
In the first way, the outcomes are not equally likely.
In the second, they are.
In \(10^6\) simulations:
num_12 = 0
num_11 = 0
for t in range(1000000):
faces = [1,2,3,4,5,6]
D1 = random.choice(faces) # roll 2 dice
D2 = random.choice(faces)
if D1 + D2 == 11:
num_11 += 1
if D1 + D2 == 12:
num_12 += 1
fig, ax = plt.subplots()
ax.pie([num_11, num_12], labels=["11","12"], autopct='%1.2f%%')
plt.show()
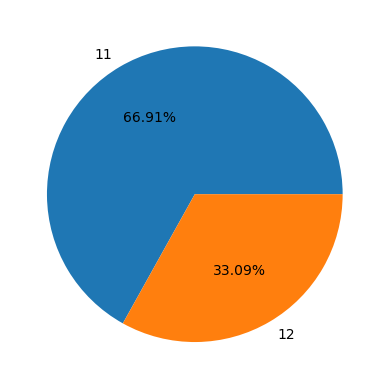
The 1600’s mathematician Gottfried Wilhelm Leibniz (one of the inventors of calculus) asserted that the answer to the above was True, even though we have just convinced ourselves that it is false.

Leibniz. Image from Wikipedia.
A fix#
It is sometimes easiest to work with an experiment where the outcomes are equally likely.
To make sure the outcomes are equally likely, it is useful to think of the components of your experiment as having labels.
If you are rolling \(k\) identical dice, label the dice as dice \(1,\ldots,k\).
If you are sampling \(k\) things out of \(N\) things in total, you should think of each of the \(N\) things as labeled, unique objects (each one a unique snowflake).
Leibniz’s dice example#
We label the dice \(D_1\) and \(D_2\).
The outcomes are all pairs \((D_1,D_2)\) with \(D_1 \in \{1,\ldots,6\}\) and \(D_2 \in \{1,\ldots,6\}\). Each outcome is equally likely.
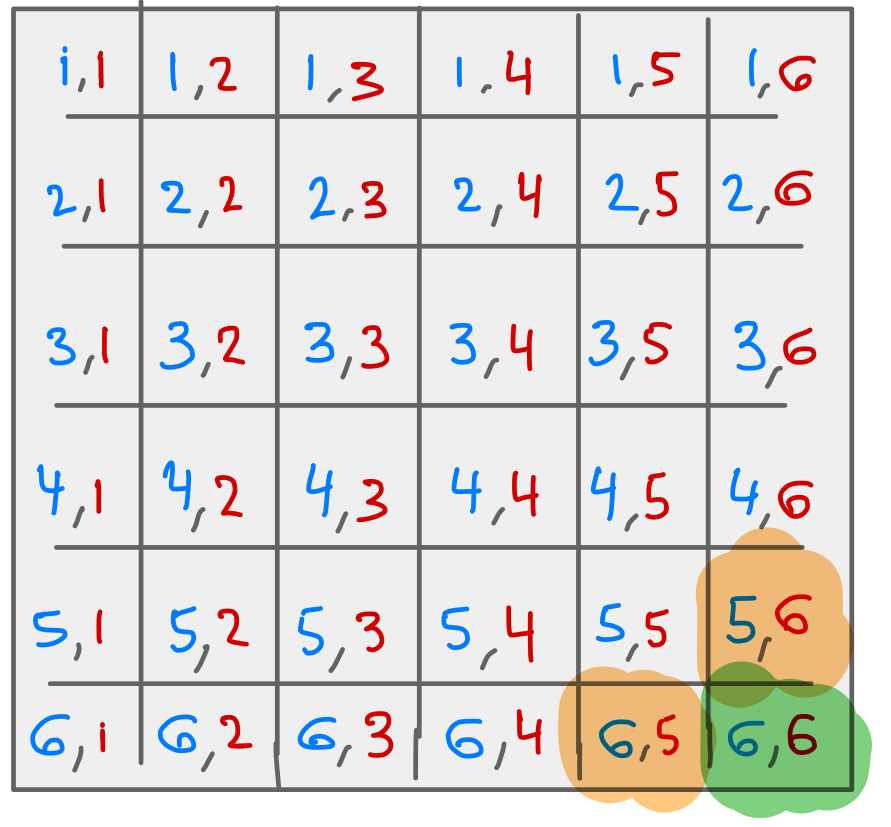
Sample space for Leibniz's dice.
The outcomes which give 11 are \((5,6)\) or \((6,5)\).
The only outcome which gives \(12\) is \((6,6)\).
What is the probability of the event that that the sum of the dice is 12?
What is the probability of the event that that the sum of the dice is 11?
Marbles and Coinflips all the way down#
Almost every experiment is equivalent to an experiment involving a bag of marbles or flipping of a (biased) coin. This can be useful for calculating probabilities!
Suppose that for each integer \(n \ge 0\), we have access to a bag of \(n\) distinct marbles, and for any \(p \in [0,1]\) we have a coin which lands on heads with probability \(p\). How can we simulate:
A poll in which we ask \(k\) out of \(n\) people if they prefer option \(A\) or \(B\)?
Each marble represents a person, labeled with the person’s name and their opinion (A or B).
Draw marbles one at a time from the bag, without putting them back, until you have \(k\) marbles, and count how many of them are labeled with opinon A.
An NBA team (say, the Warriors) playing \(5\) games against \(5\) different oponents?
Suppose that in a match agains team \(i\), the Warriors have probability \(p_i\) of winning.
We flip coins with probability \(p_1\), then \(p_2\), … \(p_5\), and if the \(i\)th coin comes up heads this simulates a win in the \(i\)th game.
A randomized controlled trial, in which we choose \(m\) sick people at random for the control group, \(m\) sick people at random for the treatment group, treat the treatment group, and observe who gets better? Use probability to model not only the selection of people, but also whether or not they get better.
Let \(n\) be the number of sick people in the population; consider a bag with \(n\) marbles, each labeled with the name of a sick person.
We sample \(m\) marbles from the bag without replacement and put them in the control group.
We sample \(m\) marbles out of what remains in the bag and put them in the treatment group.
Suppose that if person \(i\) gets treated, then they get better with probability \(p_i\), and if not treated, they get better with probability \(q_i\). For each marble \(i\) that was selected, flip a coin with heads probability \(p_i\) if it was drawn in the treatment group, and a coin with heads probability \(q_i\) if it was selected for the control group.
The number of people who got better in each group is the number of coinflips for the group that came up “heads.”
Axioms of probability#
The following facts are called the axioms of probability.
The probability of any event is always non-negative.
The probability of some outcome happening is \(1\).
For an event \(A\), \(\Pr[A] = 1-\Pr[\bar{A}]\).
Convince yourself of each of these statements, write a quick logical argument on your worksheet.
Complements#
Sometimes, it is easier to compute the probability that an event does not happen.
Example: What is the probability of the event \(A\) that if I roll two dice, at least one of them shows an even number?
This is the same as \(1-\Pr[\overline{A}]\), where \(\overline{A}\) is the event that both are odd. There are only \(3 \times 3\) outcomes where both rolls are odd, and \(6 \times 6\) outcomes in total. \(\Pr[\overline{A}] =\frac{3 \times 3}{6 \times 6} = \frac{1}{4}\).
\(\Pr[A] = 1 - \Pr[\overline{A}] = \frac{3}{4}\).
