Lecture 14: When means mislead#
STATS 60 / STATS 160 / PSYCH 10
Concepts and Learning Goals:
Summary statistics only give a snapshot of a dataset, sometimes incomplete.
Features that can influence the mean:
Multi-modality
Skewness
Outliers
Variability (sort of)
Features that can influence standard deviation:
Multi-modality
Outliers
Just a snapshot.#
Summary statistics give a snapshot of a dataset.
So far we’ve discussed the following summary statistics: mean, median, standard deviation, and quantiles.
Some information is always better than nothing. But very different datasets can have the same summary statistics!
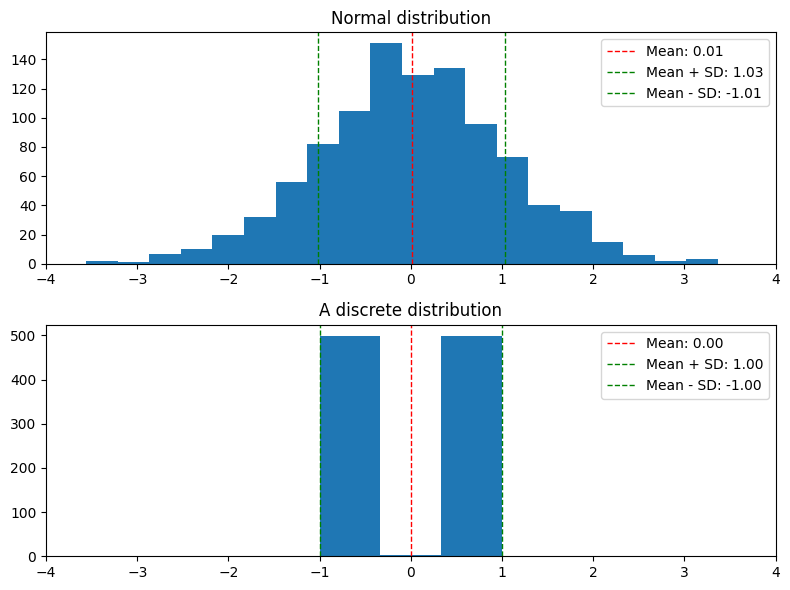
Today we study how features of the data can influence summary statistics.
The Mean#
The mean is good#
The mean is one proxy for the “center” of the distribution.
A common tendency is to conflate “center” with “typical value”.
In some cases, this is reasonable.
Example (Scientific Experiments): You do \(n\) independent experiments to measure the value of a fixed, bounded quantity \(Q\), e.g.:
The concentration of microplastics in the Palo Alto water supply
The plasticity of a protein
The fraction of students who think a hot dog is a sandwich
Because of error, each experiment is a possibly noisy measurement of \(Q\).
In Unit 4, we’ll make a rigorous argument that in such an experiment, the mean of our dataset is very close to \(Q\), as long as \(n\) is large enough.
But many types of data we encounter are not like this!
Misleading means#
Features of a dataset that can “throw off” the mean as a measure of the “typical” value:
Multi-modal data
Skewed and heavy-tailed distributions
Outliers
High variability
Misleading means 1: multi-modal data#
The mode of a dataset is the value that appears most frequently, or the highest point in the histogram.
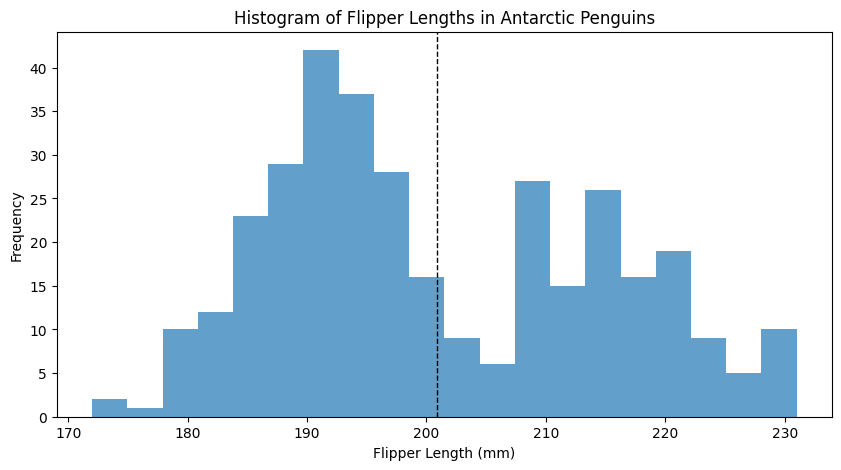
Sometimes, people use the term more loosely, using “mode” to refer to a “lump” in a histogram.
A common intuition is that that the mean is roughly where the mode is.
In some cases, like the “independent experiments” case, this is true.
But sometimes, a dataset is naturally multi-modal.
Multi-modal data#
Many datasets can be naturally decomposed into natural subsets.
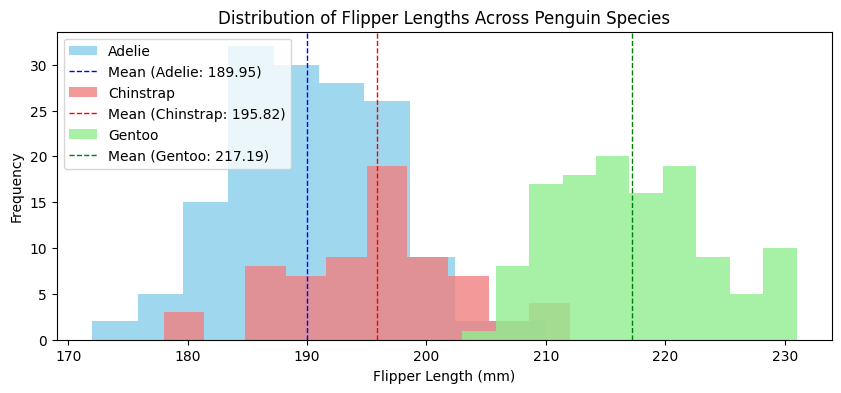
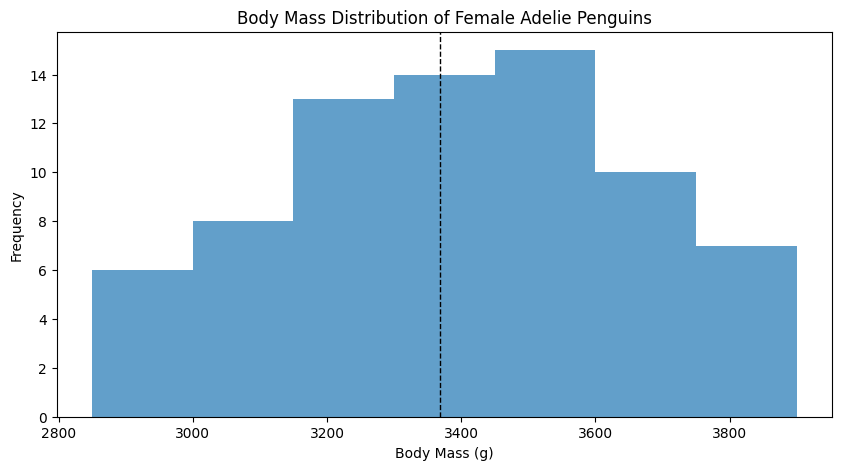
Within each subset, there is only one mode.
In this case, within that subset, the mean and mode do match!
Effects of multiple modes on the mean#
In a multi-modal dataset, the dataset’s mean value lies between the means of the different modes.
In that case, it is not representative of a “typical” sample.
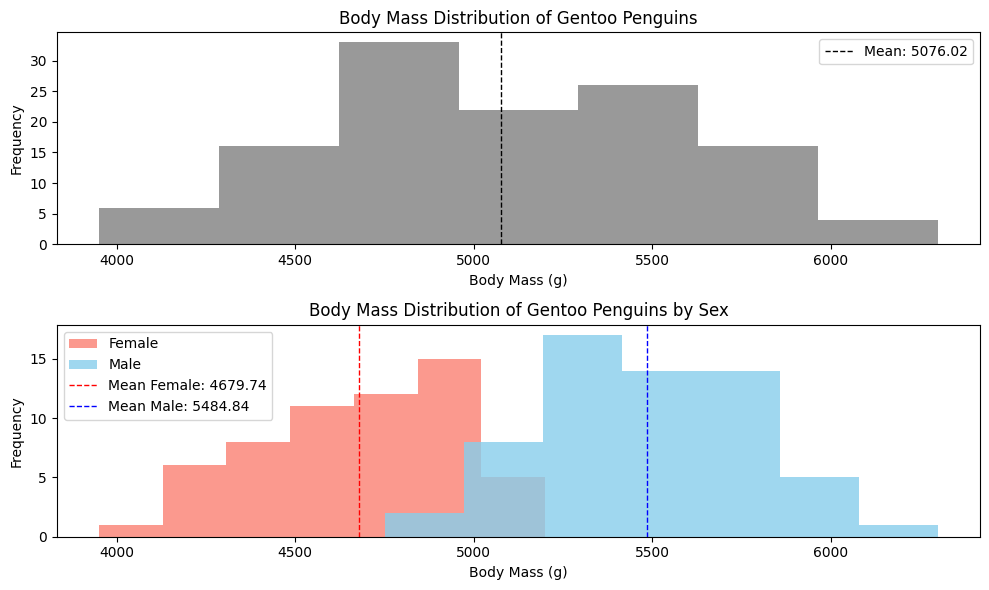
Here, the mean for the entire dataset is on the large end for a female, but on the small end for a male.
How does multi-modal data affect other statistics?#
Question: Should the median also be influenced by multiple modes?
Question: Should quantiles be influenced by multiple modes?
Question: Should the standard deviation be influenced by multiple modes?
Yes! In the sense that the aggregate data’s median, quantiles, and standard deviation do not reflect what is going on in the specific modes.
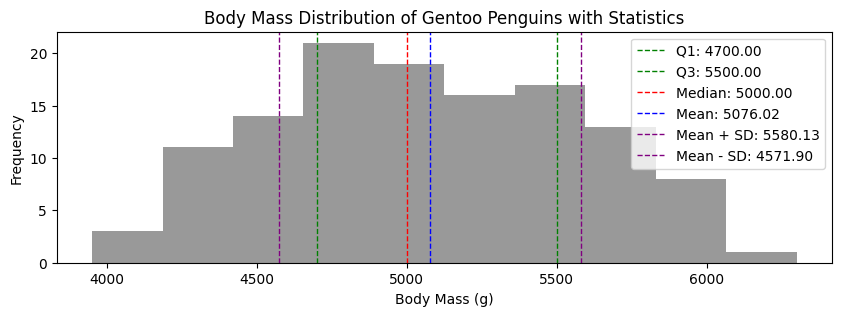
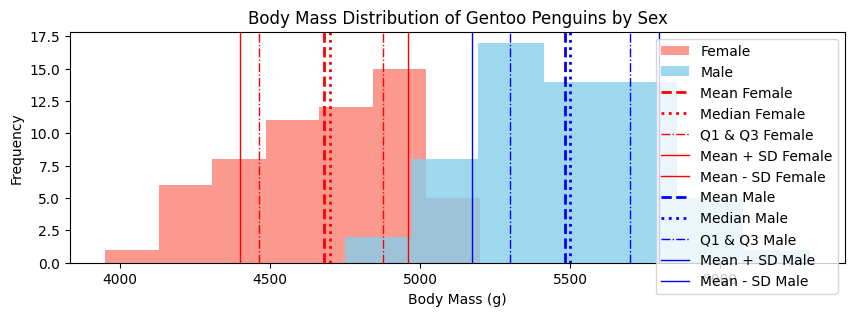
Why does this matter?#
Many times, the mean (and other summary statistics) are used to make decisions.
When decisions are based on statistics of all of the data, instead of mode-by-mode, then it might not be the right decision for everyone.
Here is a synthetic example:
A medical researcher at a hospital records the duration of symptoms for a new disease.
The average amount of time the symptoms are experienced is 20 days.
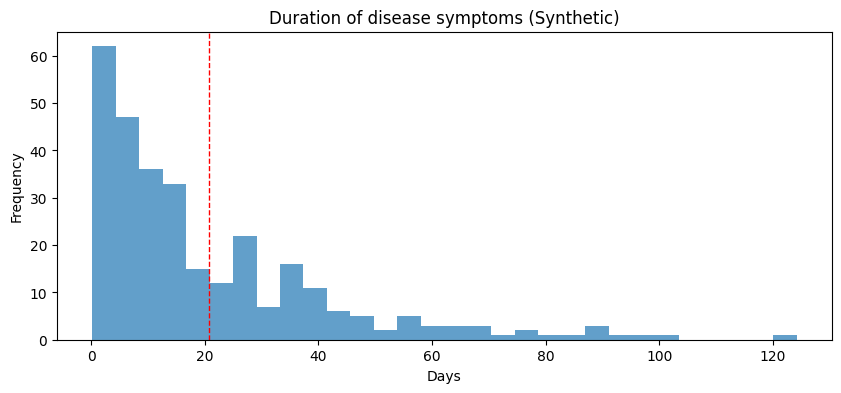
The data does not look obviously multimodal.
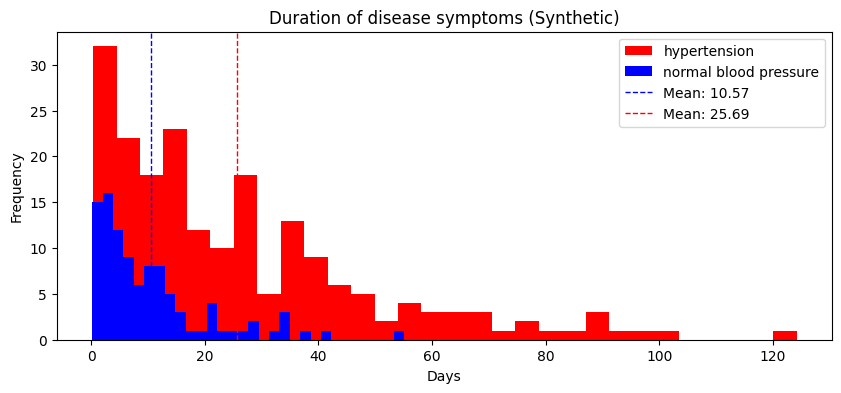
But suppose we separately analyze the data for patients with and without hypertension; in that case, we see that the average duration of symptoms for patients without hypertension is much shorter:
Question: How is the phenomenon of multi-modal data related to conditional probabilities?
A real example?#
Consider this plot of time-to-onset for COVID symptoms:
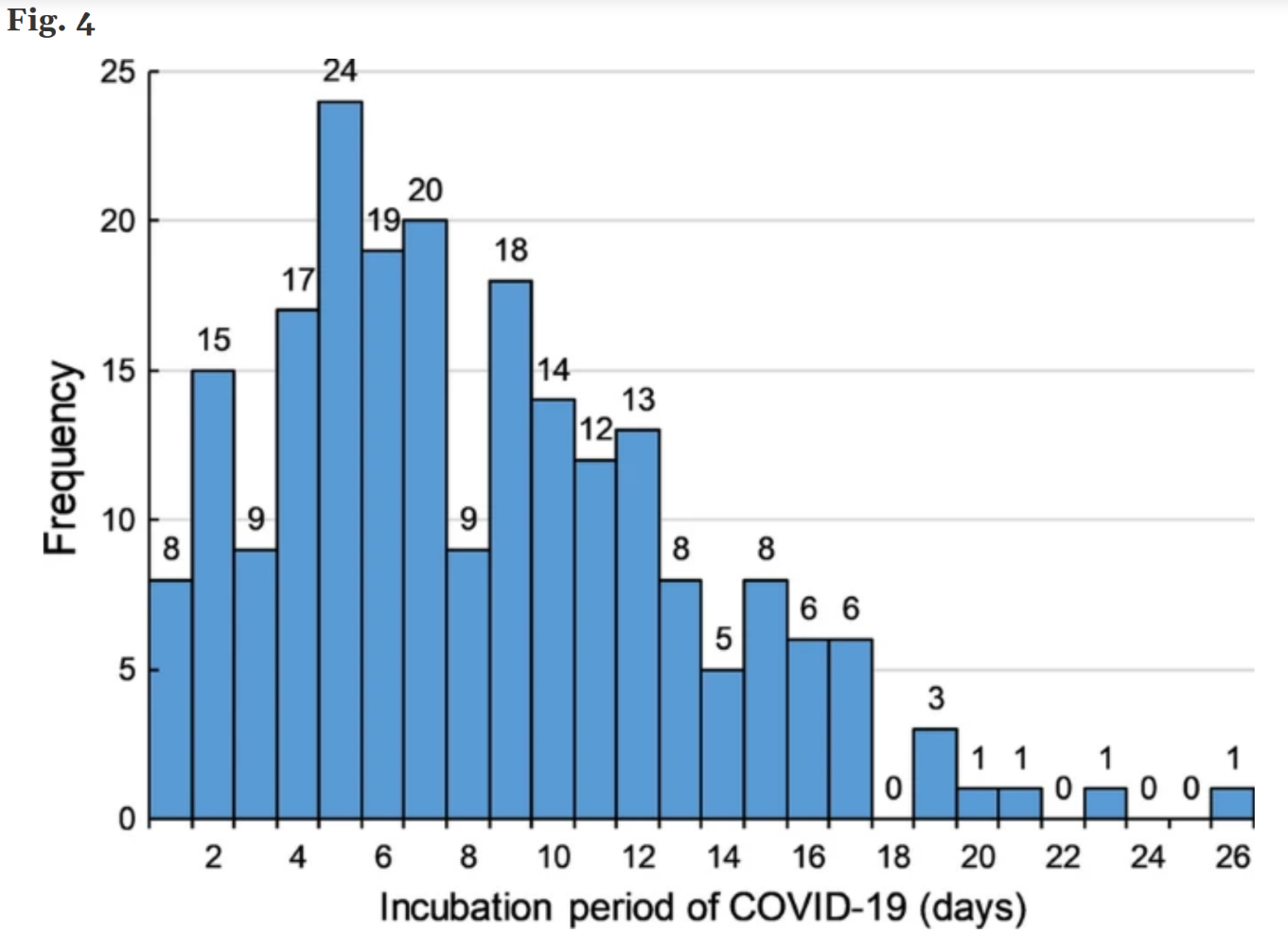
Question: Could this data be multimodal? Suppose we make recommendations for isolation time after close contact based on this data—in what sense is this problematic? What are the tradeoffs that we have to make?
Misleading Means in the Media#
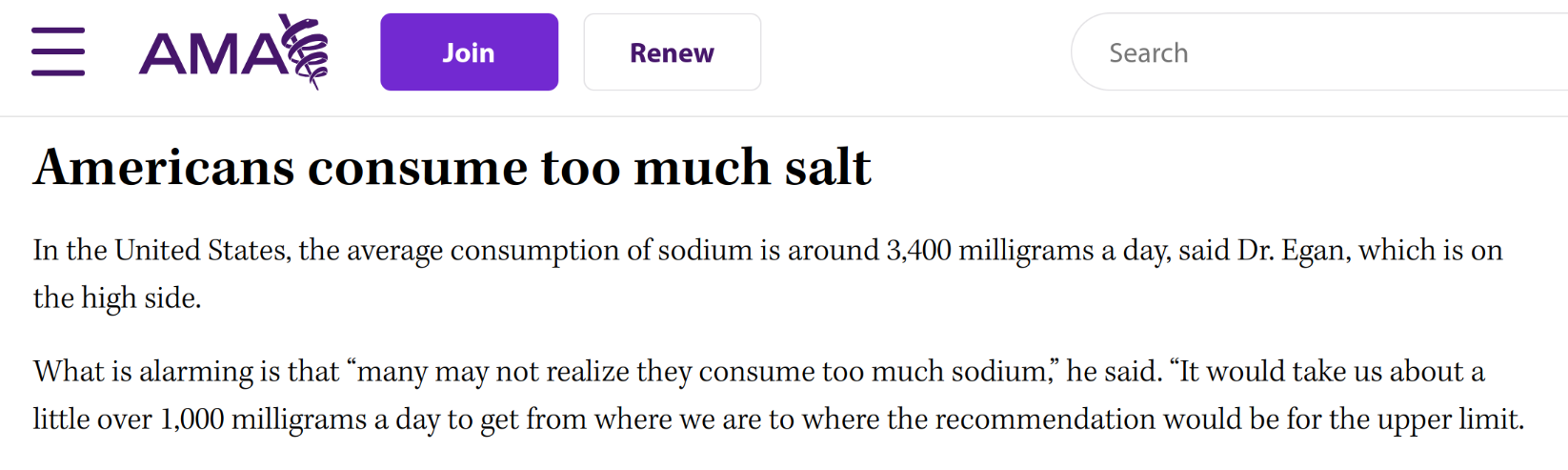
Is this representative of most people? Could the data be multimodal? Is there a lot of variability?
A closer look#

A CDC study suggests that:
The data is multimodal: women consume about 3000 mg per day on average, and men consume about 4000 mg per day on average.
Variability is limited, in the sense that 86.7% of American adults are eating more than the recommended 2300 mg. Note that this leaves open the possibility that all 11% of Californians are eating the recommended amount :P
The conclusion that Americans are eating more salt than the medical community suggests they should is still valid. But the 3400 mg figure is still misleading.
Misleading means 2: skew#
Even when the distribution has only one mode, it can be skewed.
Colloquially, this means that the histogram “stretches out” to the left or the right.
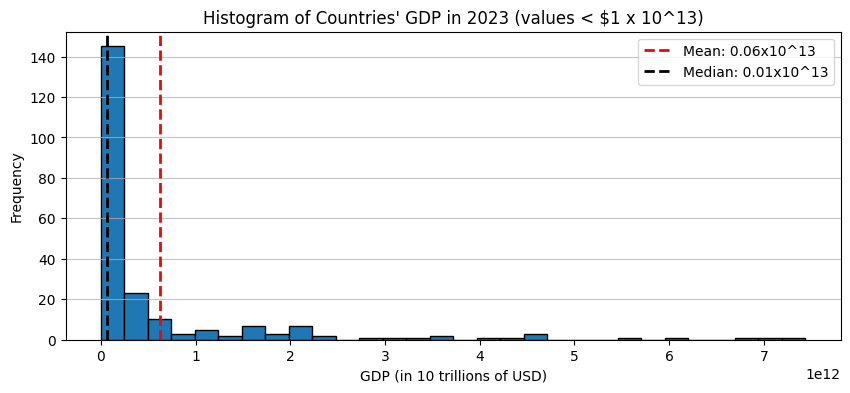
There are several quantitative measures of skewness; I don’t expect you to know any of them, only the concept of skew.
Sometimes people also say the distribution is heavy-tailed (because the stretched out part looks like a tail?).
Examples of data that tend to be skewed#
Skewed to the right:
Incomes, GDP, number of awards won, views or clicks online: “the rich get richer”
Waiting times (e.g. time between earthquakes or volcanic eruptions)
Sizes of some natural objects (lakes, rocks, mineral deposits) Also an example of the rich get richer or poor get poorer?
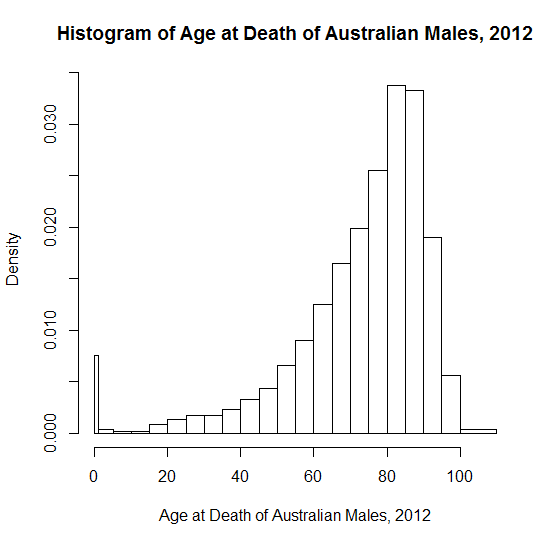
Skewed to the left:
Age of mortality
Exam scores
Effects of skew on the mean#
If a distribution is skewed to the right, then typically the median/mode will be smaller than the mean.

If a distribution is skewed to the left, then typically the median/mode will be larger than the mean.
The gap between the mean and the median is one quantitative measure of skew!
Misleading means 3: outliers#
Outliers (abnormally large or small values) can move the mean away from the median or mode.
Outliers and skew are related: outliers do skew the distribution.
The distinction is usually that we think of outliers as anomalies, whereas skew can be a “natural” property of the data.
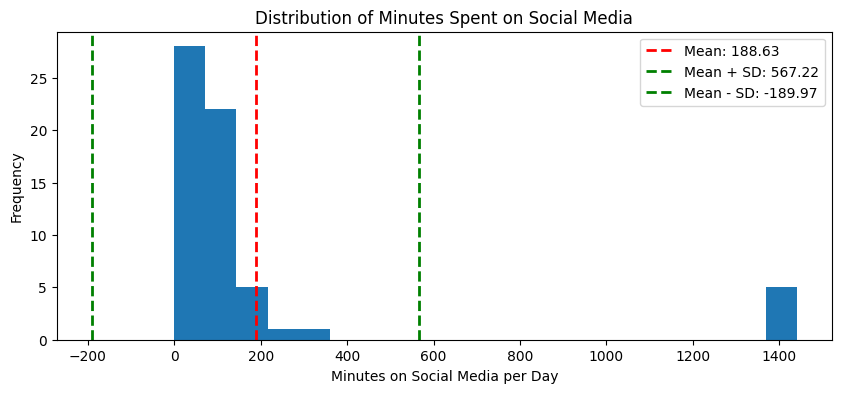
This is a histogram of responses to the in-class survey question “How many minutes per day do you spend on social media?”
One of you replied “all,” that is, \(60 \times 24 = 1440\). This creates a huge outlier, and the mean and standard deviation end up being huge.
Misleading means 4: high-variability datasets#
If the variability of a dataset is high, then the mean is no longer representative of a “typical” sample.
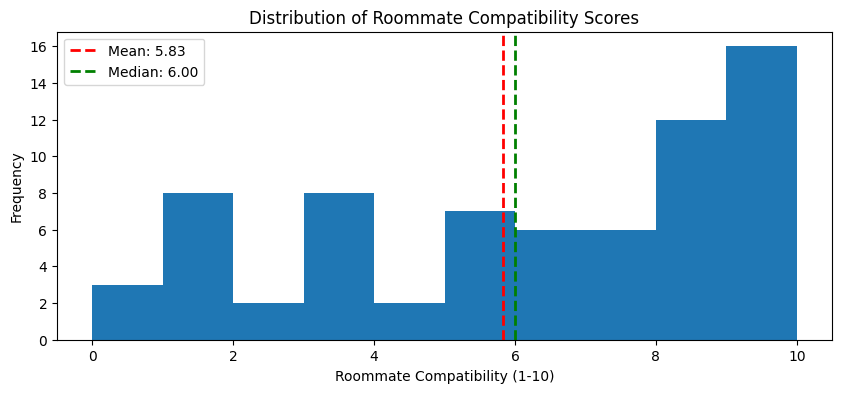
This is a histogram of responses to the course data survey question “Roommate compatibility Freshman year, on a scale from 1-10”.
The mean and median are pretty close.
But the variability is really high; in my opinion, 5.83/10 is not representative.
More high-variability datasets#
Another example of a situation where the mean is not necessarily representative is in gambling:
Flip a fair coin for \(\$300\).
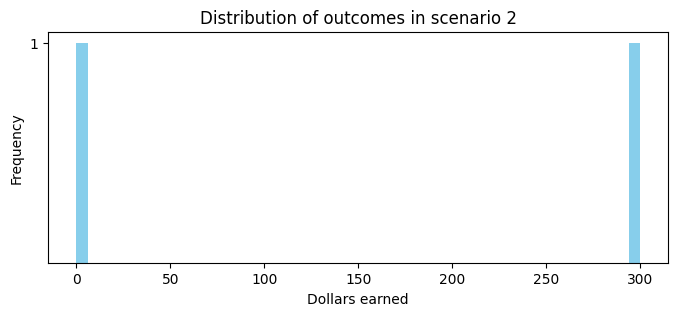
Remember the mean is \(\$150\).
Neither situation is really like the mean.
Standard deviation#
The standard deviation gives confidence intervals#
The standard deviation \(\sigma\) is a proxy for “average distance to the mean,” \(\bar{x}\).
As discussed briefly on Monday, the standard deviation always gives us a valid estimate of how “spread out” our distribution is.
If we sample \(x_i\) uniformly at random from our dataset \(\{x_1,\ldots,x_n\}\), then
That is, at least a \(1-\frac{1}{t^2}\) fraction of \(x_i\) are within a window of size \(t \sigma\) around \(\bar{x}\).
This is true no matter what, by a fact called Chebyshev’s inequality.
Example: \(\approx 90\%\) of the data are within \(3.3 \sigma\) of \(\bar{x}\).
The technical term here is that $(\bar{x} - t \sigma, \bar{x} + t\sigma)$ is a $1-\frac{1}{t^2}$ **confidence interval** for $x_i$, more on this later.The standard deviation can be an overestimate#
We know for sure that \(\approx 90\%\) of \(x_i\) are in the window \((\bar{x} - 3.3\sigma, \bar{x} + 3.3\sigma)\).
Many times this is a dramatic overestimate!
Outliers#
Outliers and heavy tails can make the standard deviation really large.

In this case, the standard deviation is, qualitatively, an overestimate of the variability.
Question: what should we use as an alternative measurement of variability?
Recap#
Summary statistics are just a snapshot.
Different distributions can have the same summary statistics.
The mean and standard deviation behave differently than we expect if the data has
Multi-modality
Skewness
Outliers
What does this mean for us?
The bottom line is that any summary statistic is just a summary; often useful, but sometimes incomplete. You have to look at the data to be sure.
