Lecture 13: Variability

Lecture 13: Variability#

STATS 60 / STATS 160 / PSYCH 10

Concepts and Learning Goals:

Variability of distributions
Intuition for variability from histograms
Common measures of variability:
- Variance and Standard Deviation
- Quantiles

Announcements:

Variability#

In the last lecture, you learned about them mean and median.

Both measure where the center of a distribution (the data) is, for different notions of centering.

But many times, we don’t just care where the center of the distribution is; we also want to know about the variability of the data.

Are most of the samples close to the center (mean/median), or not?
What is the “typical range” the data falls into?

Question: think of examples of scenarios where you care not only where the data is centered, but also what the variability is.

Medicine: you know the average life expectancy, given a diagnosis. But what are the best/worst case scenarios?
Exams: you know the class average, and you know your score. But how do you really compare to the rest of the class?
Investments: you are trying to decide if you should invest in a stock. You know the historical average annual rate of return. But is it possible that there will be a big loss?

Example 1: daily temperatures in different cities#

Recounting the example from last lecture, below are the overlayed histograms of daily average temperatures in two cities in the last year.

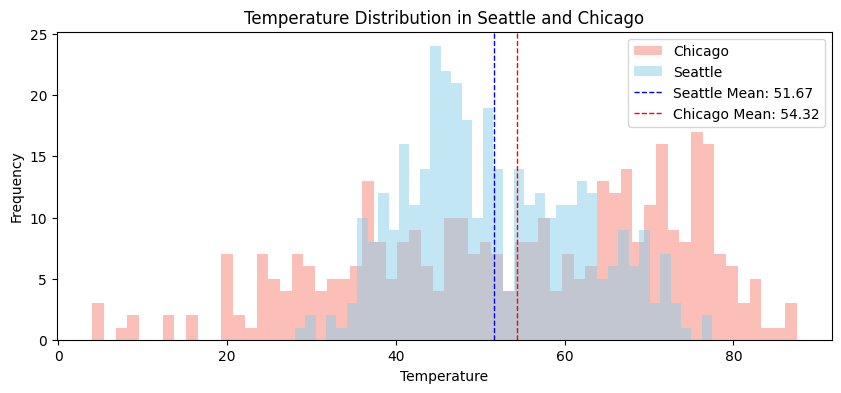
The means of the two cities are very close, but the distributions are very different.

Qualitatively, the temperature in Chicago exhibits greater variability.

Example 2: stock prices#

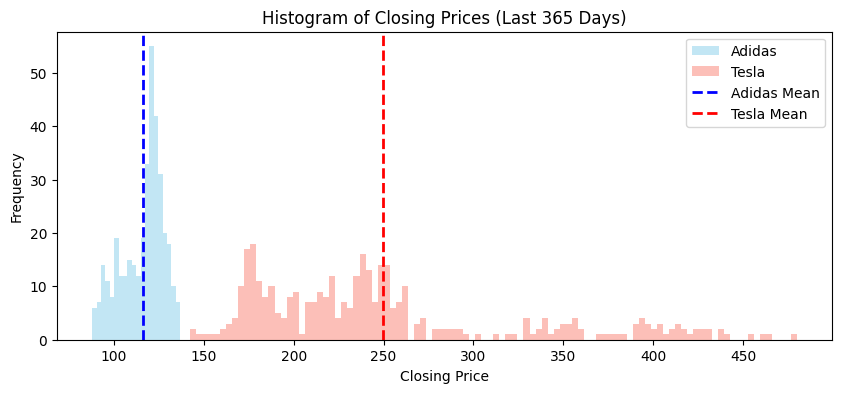
These histograms show the daily closing prices of Adidas and Tesla stock for the last 365 days.

Stock prices#

Here, the means are different, so it is harder to compare the data.

Rescaled#

If we rescale the Adidas stock so that the mean is the same, the comparison is clearer.

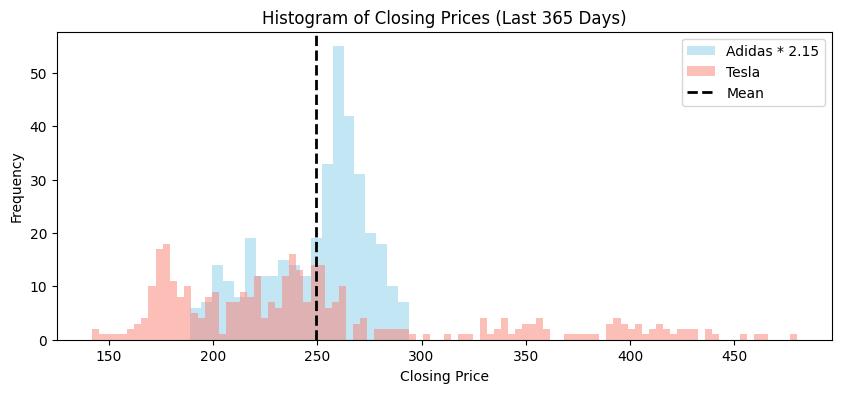
Qualitatively, the TSLA price exhibits greater variability.

How should we measure variability?#

We saw two examples of distributions with similar means, but different levels of variability.

Question: how would you quantitatively measure variability?

Variance#

A common quantitative summary of variability is the variance.

The variance is the average squared distance to the mean, $\bar{x}$:

\[ \overline{\sigma^2} = \text{variance} = \frac{(x_1-\bar x)^2 + (x_2 - \bar x)^2 + \dots + (x_n - \bar x)^2}{n} \]

(Remember the mean $\bar{x}= \frac{x_1 + x_2 + \cdots + x_n}{n}$)

Question: Calculate the variance of the rowers’ heights. What are the units?

Standard Deviation#

The standard deviation is the square root of the variance:

\[ \bar \sigma = \text{standard deviation} = \sqrt{\bar \sigma^2}. \]

If the data has the units $u$, then the variance has the units $u^2$. So the units of the variance are incompatible with the units of the data.

For this reason, if you want a measure of variability that you can compare to the mean, you should use the standard deviation rather than the variance.

Question: Calculate the standard deviation of the rowers’ heights.

Variability and risk#

Suppose someone offers you a choice between:

A gift of $100
The chance to flip a fair coin for $300.

What would you choose, and why?

Question: calculate the mean and standard deviation of your earnings in each scenario.

Scenario	Mean	Standard Deviation
1	$100	$ 0
2	$150	$ 150

Scenario 2 is a probabilistic situation; we can think of this as a distribution containing the two outcomes, both equally likely.

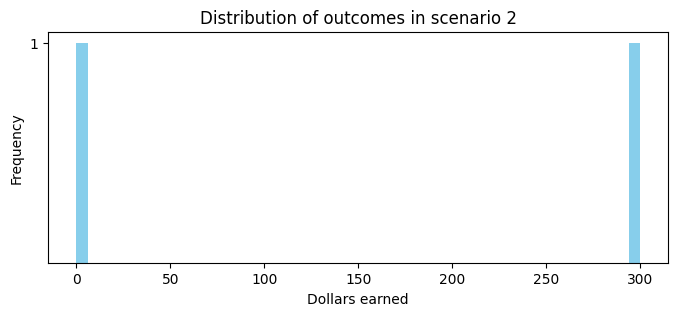
We can calculate

Example 1: variance and standard deviation of daily temperatures#

Mean and Standard Deviation in temperature for the last 365 days:

City	Mean Temperature	Standard Deviation
Seattle	$51.7^{\circ} F$	$10.3^{\circ} F$
Chicago	$54.3^{\circ} F$	$19.0^{\circ} F$

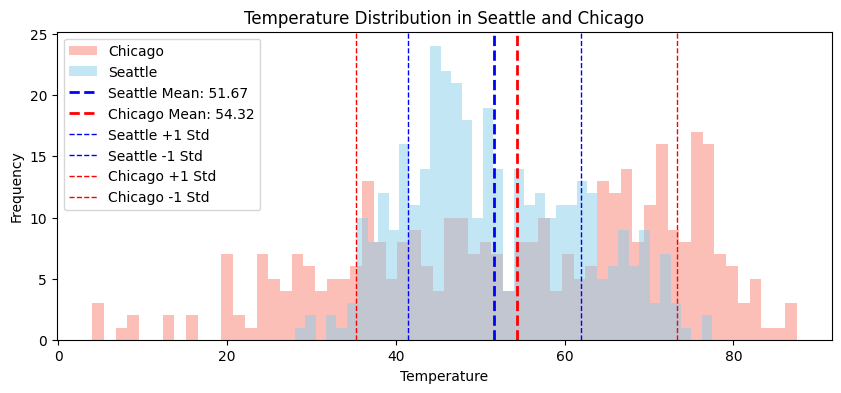
The standard deviation of temperature in Chicago is about twice as much as that of Seattle.

Example 2: variance and standard deviation of stock prices#

Mean and Standard Deviation in closing value for the last 365 days:

Stock	Mean Value	Standard Deviation
TSLA	$249.60	$75.02
ADDYY	$116.10	$11.63

The standard deviation of Tesla stock is about 30% of its mean value.

The standard deviation of Adidas stock is about 10% of its mean value.

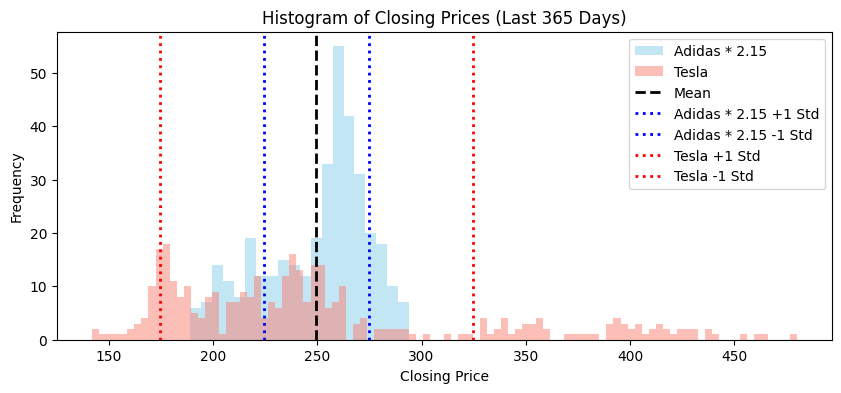
Aside: the ratio of the standard deviation to the mean only makes sense as a measurement of variability for non-negative data.

Discussion#

Questions:

Do you think the standard deviation is a satisfying measure of variability? What is it conveying? What is it not conveying?
Suppose you know the mean and standard deviation. Can you infer that a “typical” sample is within 1 standard deviation of the mean?

Quantiles#

Quantiles tell us the fraction of the data that falls in each range. They give us a more complete picture of variability.

The $k$-quantiles of a distribution are the $k-1$ numbers which partition the histogram into $k$ equal-sized parts:

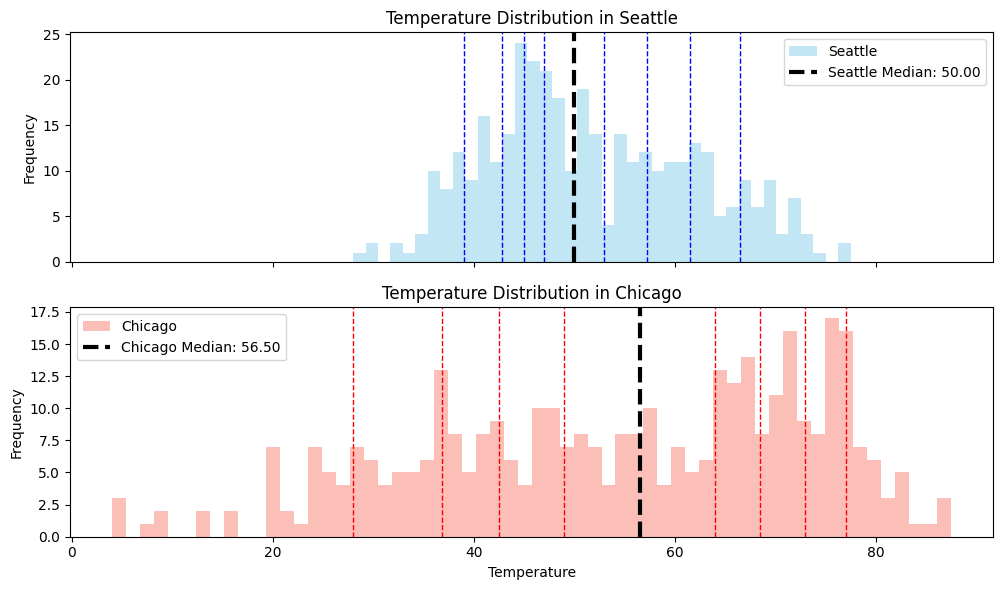
Depicted here are the $10$-quantiles, also known as deciles.

Other commonly used quantiles are the quartiles ($4$-quantiles), and percentiles ($100$-quantiles).

Using quantiles to measure variability#

Question: How can we use quantiles to measure variability?

We can measure distance between quantiles, or between quantiles and the mean.

For example, the distance from the $10$th percentile to $90$th percentile:

City	Mean Temp	Std. Dev	10th Percentile	90th percentile	10-90 percentile window
Seattle	$51.7^{\circ F}$	$10.3^{\circ F}$	$39^{\circ F}$	$66.5^{\circ F}$	$27.5^{\circ F}$
Chicago	$54.3^{\circ F}$	$19.0^{\circ F}$	$28.0^{\circ F}$	$77.0^{\circ F}$	$49^{\circ F}$

Another way to think about quantiles#

Question: How does the information we get from the standard deviation differ from the information we get from the quantiles?

The quantiles tell us not only the average distance to the mean, but also the percent of the time we can expect to be close to the mean.

For example: 80% of data points in the histogram fall between the 10th and 90th percentile.

Question: Why?

City	10th	90th	Window Size
Seattle	$39^{\circ F}$	$66.5^{\circ F}$	$27.5^{\circ F}$
Chicago	$28.0^{\circ F}$	$77.0^{\circ F}$	$49^{\circ F}$

In each city, you can reasonably expect that 80% of the time, the temperature will be in the 10-90th percentile window.

This also gives us a sense of the variability.

Recap#

Concept of variability
Common measures of variability:
- Variance and Standard Deviation
- Quantiles

City	Mean Temp	Std. Dev	10th Percentile	90th percentile	10-90 percentile window
Seattle	\(51.7^{\circ F}\)	\(10.3^{\circ F}\)	\(39^{\circ F}\)	\(66.5^{\circ F}\)	\(27.5^{\circ F}\)
Chicago	\(54.3^{\circ F}\)	\(19.0^{\circ F}\)	\(28.0^{\circ F}\)	\(77.0^{\circ F}\)	\(49^{\circ F}\)

City	Mean Temperature	Standard Deviation
Seattle	\(51.7^{\circ} F\)	\(10.3^{\circ} F\)
Chicago	\(54.3^{\circ} F\)	\(19.0^{\circ} F\)