Lecture 6: Conditional probability

Lecture 6: Conditional probability#

STATS 60 / STATS 160 / PSYCH 10

Announcements:

A new section is now open at 10:30! Please attend that section.
On Monday, I will be giving a talk at the University of Washington. Fabulous TA Michael Howes will sub for me.

Partial information#

In many situations involving randomness or uncertainty, we get partial information before knowing the complete outcome.

Examples:

Election night: the votes are being counted, and counties report data one at a time. How can we update our forecast that your favorite candidate wins based on the partial count?
Stock market: we made an investment based on a prediction that a company will do well. How can we update our forecast based on news stories?
Weather: your prediction for whether it will rain today is improved when you look out the window and see if it looks cloudy.
Texas Hold ‘Em: In this variant of poker, each player’s hand is made up of two private “hole” cards, and 5 shared “community” cards which are revealed in stages. As the community cards are revealed, you know more about how strong your hand is.

Conditional probability tells us how to update probabilities based on partial information.

Conditional probability#

For events $A,B$, the conditional probability of $A$ given $B$ is the probability that $A$ happens, given that we know $B$ happens.

Example: In poker, your own hand gives you information about other players’ hands!

Let $A$ be the event that your rival has at least one ace.

Let $B$ be the event that your $5$-card hand has all $4$ aces in it.

\[\Pr[A] = 1-\Pr[\text{rival has 0 aces}] = 1 - \frac{48 \times 47 \times 46 \times 45 \times 44}{52 \times 51 \times 50 \times 49 \times 48} \approx 0.33.\]

But if $B$ happens, then for sure your opponent cannot have any aces! So

\[\Pr[A\mid B] = 0.\]

Conditioning on the information you know can dramatically change probabilities!

Take a moment to think of an example of an uncertain situation from real life, in which you learned information $B$ that dramatically changed your estimate of whether some $A$ was going to happen.

Conditioning as “zooming in”#

Conditioning on $B$ is like “zooming in” to the set of outcomes in event $B$.

Basically, we are taking all outcomes that are not in $B$, and eliminating them from the sample space.

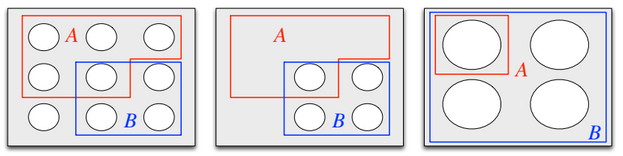
Zooming in on $B$. Image credit to Blitzstein and Hwang, chapter 2.

Consequently, we have the rule:

\[ \Pr[A \mid B] = \frac{\Pr[A \cap B]}{\Pr[B]} \]

Can you justify this formula?

Example: Two coinflips.#

Suppose I flip a fair coin twice.

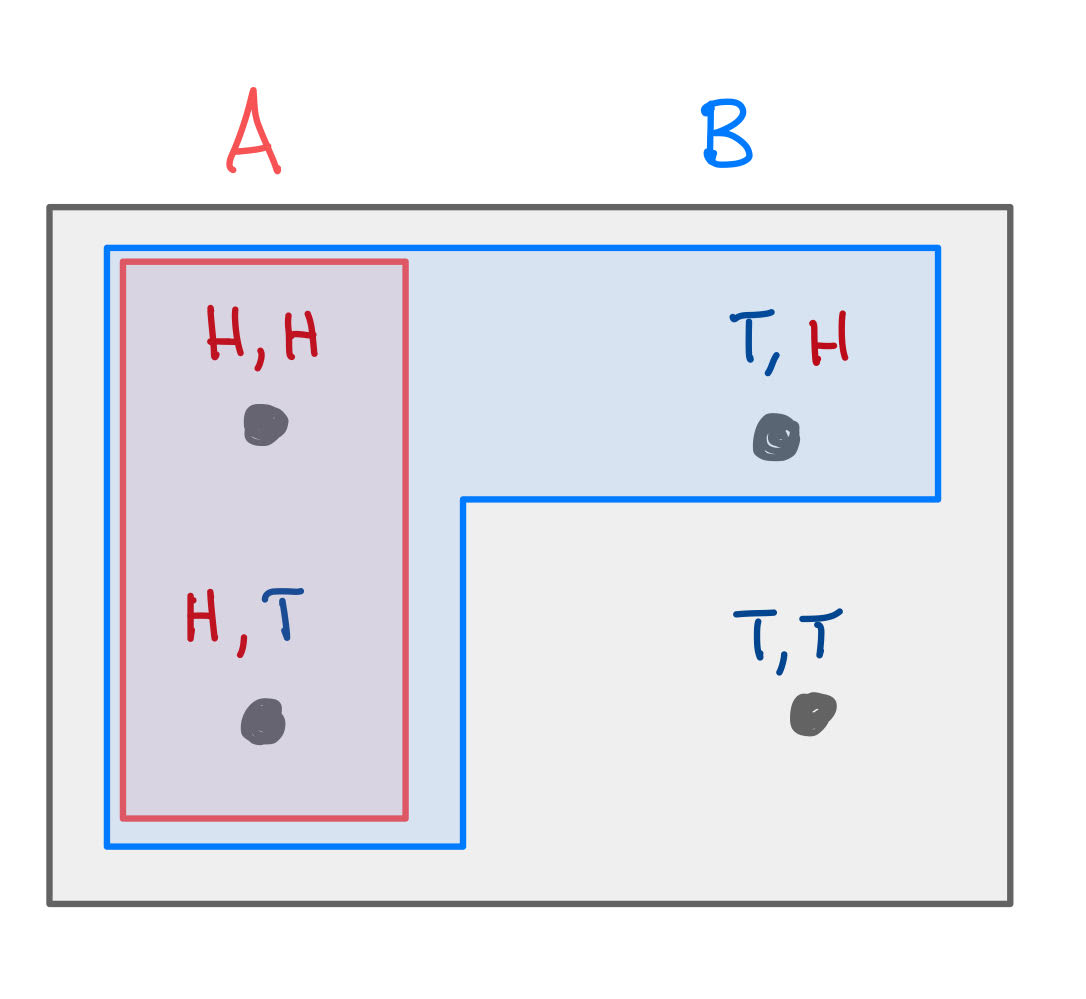
Two coin flips.

Let $A$ be the event that the first coinflip comes up heads, and let $B$ be the event that at least one of the coinflips comes up heads.

What is $\Pr[A \mid B]$?
What is $\Pr[B \mid A]$?

\[\Pr[A \cap B] = \frac{1}{2}, \qquad \Pr[A] = \frac{1}{2},\qquad \Pr[B] = \frac{3}{4}\]

Plugging in,

\[\Pr[A \mid B] = \frac{\Pr[A \cap B]}{\Pr[B]} = \frac{\frac{1}{2}}{\frac{3}{4}} = \frac{2}{3}, \quad \text{ and } \Pr[B \mid A] = \frac{\Pr[A \cap B]}{\Pr[A]} = \frac{\frac{1}{2}}{\frac{1}{2}} = 1.\]

What do you notice about this example?

$\Pr[A \mid B] \neq \Pr[B \mid A]$. This is extremely important to take note of. The mistake of confusing $\Pr[A \mid B]$ with $\Pr[B \mid A]$ is called the prosecutor’s fallacy.

Distracted driving#

Let $A$ be the event that you are driving distracted, and let $B$ be the event that you get in a car accident.

According to these stats from the National Highway Traffic Safety Administration, in recent years about $13\%$ of car accidents involve distracted driving.

How would you phrase this in the language of conditional probability?
What is $\Pr[B \mid A]$, in plain English?
What do you think happens more frequently: distracted driving, or car accidents?
Do you think $\Pr[B \mid A]$ is smaller, larger, or no different than $\Pr[A \mid B]$?

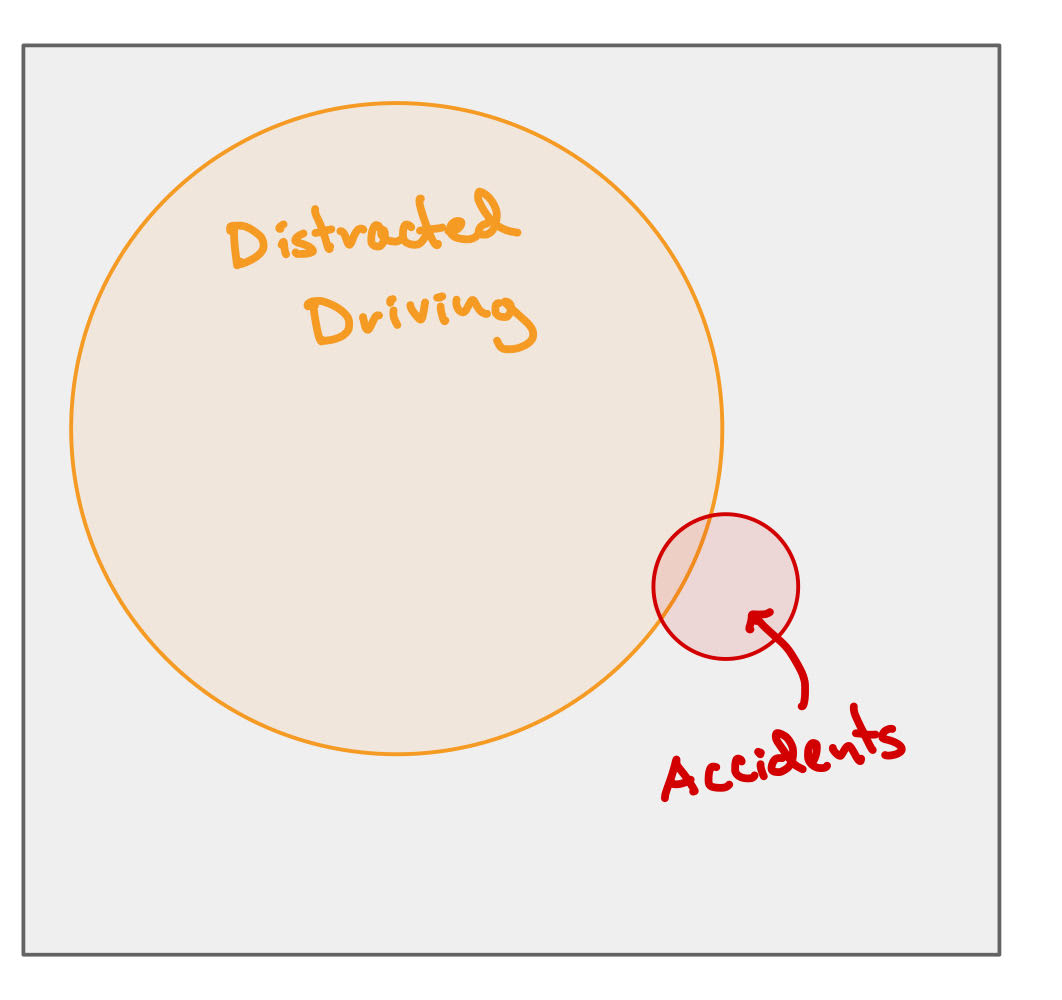
The gray box represents all instances of driving. The orange circle is the instances of distracted driving, the red is drives that result in accidents.

Answers:

\[\Pr[ A \mid B] = 0.13\]
The chance that you have a crash if you are driving distracted.
Most likely distracted driving.
Probably smaller. People drive distracted all the time. If they crashed every time, the roads would be insanely dangerous.

OJ Simpson again#

Recall the OJ Simpson trial: the prosecution gave evidence that OJ had abused his wife, the defense argued that only 1/2,500 abused women are murdered by their husbands.

Let’s see how to put this in the language of conditional probabilities.

Let $A$ be the event that a woman is abused, let $M$ be the event that the woman is murdered, and let $G$ be the event that her husband is guilty of murdering her.

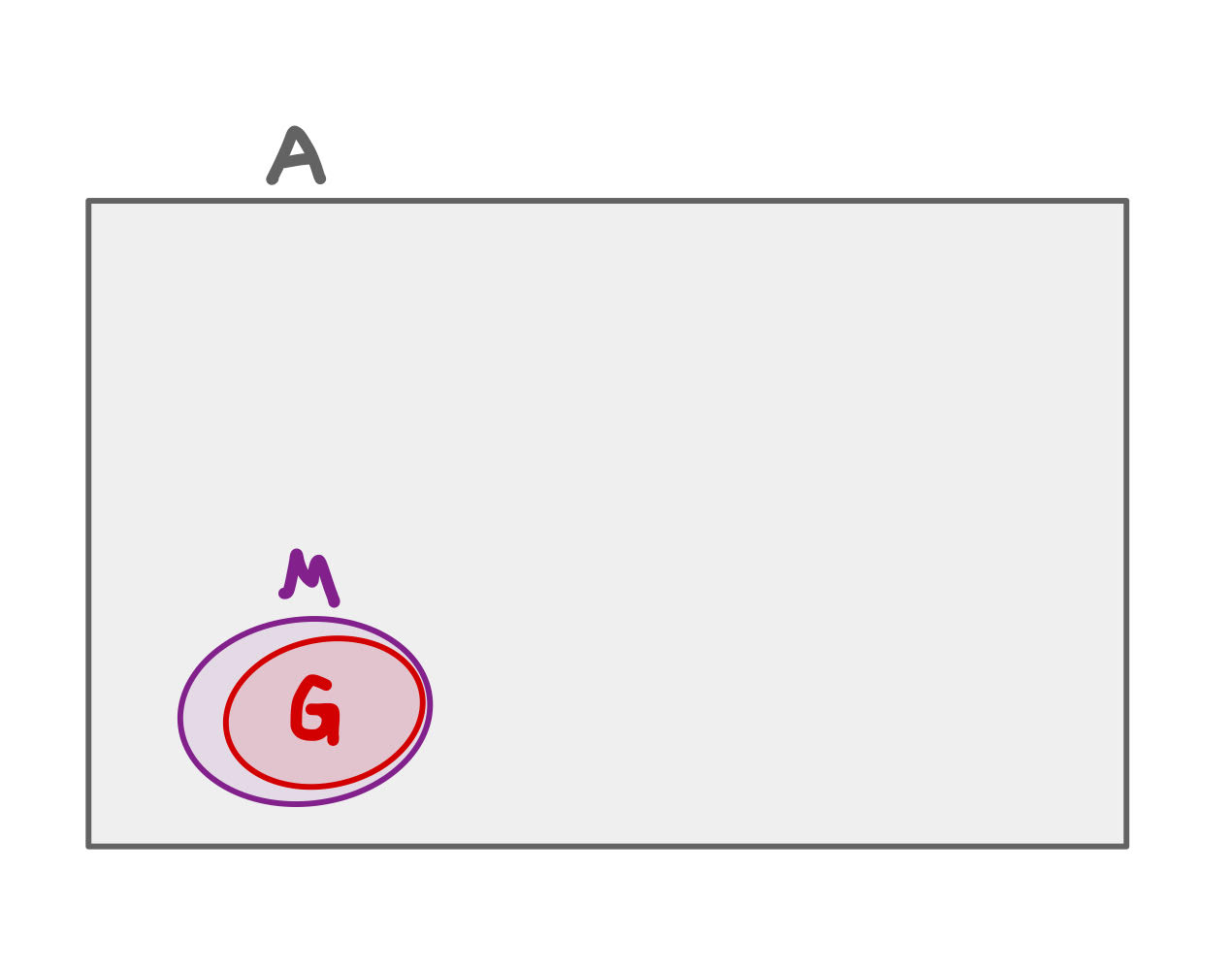
The gray rectangle represents all abused women. The small purple circle is the set of abused women who are murdered, and the red circle is the set of abused women murdered by their partners.

The prosecution gave convincing evidence that in the case of OJ’s wife, the event $A$ had occurred.
The defense argued that only $1/2500$ abused women are murdered by their husband. How would you phrase this using conditional probabilities?

\[\Pr[G \mid A] \le \frac{1}{2500}.\]

But we know that not only the event $A$ occurred, but that also $M$ occurred! When we condition on $M$ and $A$, we have that

\[ \Pr[G \mid A \cap M] = \frac{8}{9}. \]

This is an example where we dramatically underestimate a probability by failing to condition on available information! More on this in the coming lectures.

When conditioning has no impact#

Can you think of events $A,B$, where conditioning on $B$ has no impact on $A$?

Independent events#

We say $A,B$ are independent events if $\Pr[A \mid B] = \Pr[A]$.

Example: You toss a fair coin twice. Let $A$ be the even that the first toss comes up heads, and let $B$ be the event that the second toss comes up heads.

Intuitively, these events are independent; the fact that $B$ happened gives us no information about whether $A$ happened.

We can also verify that the calculation of conditional probability comes out as we would expect:

\[\Pr[A \mid B] = \frac{\Pr[A \cap B]}{\Pr[B]} = \frac{\frac{1}{4}}{\frac{1}{2}} = \frac{1}{2}\]