Lecture 5: Coincidences

Lecture 5: Coincidences#

STATS 60 / STATS 160 / PSYCH 10

Warm Up#

Let’s get some more practice with probability.

Robin’s RCT#

  1. You need to select a subset of \(n\) people to participate in a randomized control trial (RCT); suppose exactly one of these people is named Robin. You order them randomly, choose the first \(m\) of them to be in a control group, and the next \(m\) of them to be in a treatment group. The remaining people do not participate in the study. a. What is the probability that Robin participates in the study? b. What is the probability that Robin is in the control group? c. What is the probability that Robin is in the treatment group?

Counting permutations#

A permutation of \(m\) objects is any ordering of the objects from \(1\)st to \(m\)th.

The permutations of A,B,C:

A, B, C

A, C, B

B, A, C

B, C, A

C, A, B

C, B, A

If \(m\) is a positive integer, the number of permutations of \(m\) objects is denoted by \(m!\) (read “\(m\) factorial”), and is given by

\[ m! = m \cdot (m-1) \cdots 2 \cdot 1. \]

We also follow the convention that \(0! = 1\).

Can you explain why this formula is valid?

Return to Robin#

  1. You need to select a subset of \(n\) people to participate in a randomized control trial (RCT); suppose exactly one of these people is named Robin. You order them randomly, choose the first \(m\) of them to be in a control group, and the next \(m\) of them to be in a treatment group. The remaining people do not participate in the study. a. What is the probability that Robin is \(k\)th in the random order? b. What is the probability that Robin is in the control group? c. What is the probability that Robin is in the treatment group? d. Extra: If each patient is instead selected to be in the control group independently with probability \(m/n\), and in case they didn’t make it, selected to be in the treatment group with probability \(m/n\), does Robin’s chance of being chosen for the study increase, decrease, or neither?

Headcount#

  1. You flip a fair coin \(n\) times. a. What is the probability that it lands on heads every time? b. What is the probability that it lands on heads exactly \(k\) times?

Counting combinations#

The number of ways to choose \(k\) unordered labeled objects out of a total of \(n\) labeled objects is called the number of \(k\)-combinations of \(n\) elements.

The \(2\)-combinations of A,B,C,D (note order doesn’t matter):

A, B

A, C

A, D

B, C

B, D

C, D

We use the notation \(\binom{n}{k}\), also called the \(k\)th Binomial Coefficient of \(n\). We also have the formula, for \(k \le n\),

\[ \binom{n}{k} = \frac{n!}{k!(n-k)!}. \]

No need to memorize this formula (you can always use the expression \(\binom{n}{k}\), and have the computer do calculations for you), but it’s cool to know why it arises.

Can you explain why this formula is valid?

Headcount again#

  1. You flip a fair coin \(n\) times. a. What is the probability that it lands on heads every time? b. What is the probability that it lands on heads exactly \(k\) times? c. Challenge: What is the probability that the number of heads is even? Find the simplest explanation that you can.

Scrutinizing coincidences with probability#

You observe something that seems unexpected.

Is it a freak occurence?

Is it a sign of some mysterious pattern?

How likely is that this occurred “by random chance”?

Birthday Problem#

Question

What do you think is the probability that two people in this room share a birthday?

Birthday Problem Activity#

A calendar is coming around the room. When the calendar gets to you, circle your birthday. If your birthday is already circled, then we have a match!

If your birthday is circled, interrupt whatever we are doing, stand up, and announce that we have a match!

Meanwhile, let’s calculate the probability…

Birthday Problem Calculation#

  • How do we calculate \(P(\ge 2\text{ people share a birthday})\)?

  • What is the complement of “at least two people share a birthday”?

    • “no one shares a birthday” = “everyone has a different birthday”

Say there are \(n\) people in the room. $\( P(\ge 2\text{ people share a birthday}) = 1 - P(\text{n different birthdays}) \)$

\[= 1 - \frac{365 \cdot 364 \cdot 363 \cdot \dots \cdot (365 - n + 1)}{365^n}\]

How do we calculate this?

Using a computer.

import math
n = 85 # typical number of lecture attendees
1 - math.prod([(365-k)/365 for k in range(n)])

0.9999759973260097

This would have worked out for much smaller \(n\) too!

import math
n = 35 
1 - math.prod([(365-k)/365 for k in range(n)])

0.8143832388747153

What Assumptions Did We Make?#

  • Birthdays are equally likely to fall on any of the 365 days.

    • This is not true. More babies are born in Aug than Feb.

    • But the probability of a match is even higher if the birthdays are not equally likely.

  • Birthdays are independent, meaning that no person’s birthday gives you information about another person’s birthday.

Intuition for the Birthday Problem#

  • In a room with \(35\) people, there are \(\frac{35 \cdot 34}{2} = 1190\) pairs.

  • What is the probability that each pair shares a birthday?

    • \(\frac{1}{365}\)

  • The probability of each coincidence may be small (\(\frac{1}{365}\)), but there are many opportunities for a coincidence (\(1190\)).

What is probability that someone has your birthday?#

\[ P(\text{someone shares your birthday}) = 1 - P(\text{no one shares your day}) \]

\(\displaystyle = 1 - \left(\frac{364}{365}\right)^{n-1}\)

This is still kind of small!

n = 85 # typical number of lecture attendees
1 - math.prod([364/365 for k in range(n-1)])

0.2058260963145967

Conclusion: If someone else has your birthday, it kind of is a surprising coincidence. But if some pair of people happen to have the same birthday, it’s not that surprising.

Probability and Coincidences#

Persi Diaconis (1945-)

Stanford professor!

  • Diaconis and Mosteller (1989) define a coincidence as “a surprising concurrence of events, perceived as meaningfully related, with no apparent causal connection”.

    • Example: people in this room sharing a birthday

  • Probability can help us study whether coincidences are unsurprising or possibly meaningful.

    • Example: The probability of two people sharing a birthday is quite high, so we should not be surprised by this coincidence. Frederick Mosteller (1916-2006)

Streakiness#

In sports, streakiness refers to the phenomenon wherein players or teams seem to experience streaks of success (or failure).

  • Should we be surprised if a team wins many matches in a row?

  • Should we be surprised if a player makes many shots in a row?

Suppose every NBA player is equally good. In this case, we can simulate the experiment any player makes a shot (field goal) by a coin flip, with heads probability \(p = 0.47\) (the 2023 average scoring probability.)

  1. What is the probability that a player misses one of his next \(k\) attempted shots?

\(\Pr[\ge 1\text{ miss }] = 1 - \Pr[k\text{ buckets}] = 1-p^k\)

  1. There are \(n = 450\) players in the NBA. What is the probability that at least one of them makes his next \(k\) attempted shots?

\[\Pr(\text{ someone has $k$-streak }) = 1 - \Pr[\text{ all players miss at least one}]\]
\[= 1 - \Pr[\ge 1 \text{ miss}]^{n}\]
\[= 1 - (1-p^k)^n\]

How small is this probability?

n = 450
p = .47
for k in range(1,12):
    pr_kstreak = 1-math.exp(n * math.log1p(-p**k)) # same calc as above, but done using log1p(x) = log(1+x) for better numerical stability
    print("chance of at least one",k,"streak",pr_kstreak)

chance of at least one 1 streak 1.0
chance of at least one 2 streak 1.0
chance of at least one 3 streak 1.0
chance of at least one 4 streak 0.999999999832897
chance of at least one 5 streak 0.999970781677775
chance of at least one 6 streak 0.992380003599962
chance of at least one 7 streak 0.8982868445363079
chance of at least one 8 streak 0.6579456469703548
chance of at least one 9 streak 0.395824599635506
chance of at least one 10 streak 0.21081804257163517
chance of at least one 11 streak 0.10529472622191749

The chance of a 9-shot streak is pretty high!

Does this calculation convince you?

  • What assumptions did we make?

  • What is our model missing?

  • There are 30 teams in the NBA. Suppose we recycle the same calculation, with \(n = 30\) and \(p=1/2\), to ask about the probability of a winning streak for an NBA team, assuming all teams are equally good. Would this be valid?

A surprising “uncoincidence”#

Suppose phone numbers are chosen by choosing a random sequence of \(7\) digits in \(\{0,1,\ldots,9\}\).

Question: Is it more likely that you are assigned the phone number 358-6049 or the phone number 111-1111?

Answer: Each outcome has probability \(\left(\frac{1}{10}\right)^7\), so they are equally likely.

Why does the number 111-1111 feel like a bigger coincidence than the number 358-6049?

I think it is because we see these numbers and identify them immediately with patterns.

111-1111 represents the pattern “all digits are the same”

358-6049 represents the pattern “all digits are different”

  1. What is the probability that all the digits are the same?

  2. What is the probability that all the digits are different?

The probability that all are the same is \(10 \cdot \left(\frac{1}{10}\right)^7 = 10^{-6}\). There is one outcome for each of \(10\) digits, all equally likely.

The probability that all are different is \(10 \cdot 9 \cdots 3 \times \left(\frac{1}{10}\right)^7 \approx 6 \cdot 10^{-2}\). There are \(\frac{10!}{3!}\) outcomes, all equally likely.

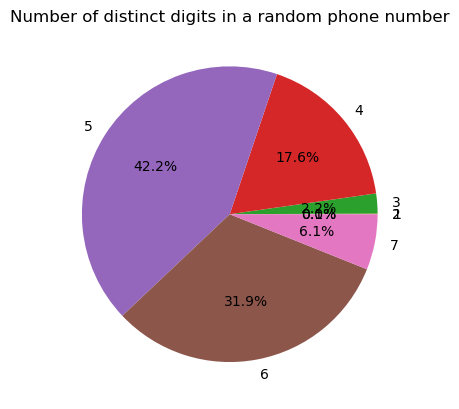
If you’re curious what the most likely number of distinct digits is:

import numpy as np
import matplotlib.pyplot as plt

frequency = np.zeros(7)
for t in range(10**5):
    x = np.random.choice(10, 7)
    k = len(set(x)) # count how many distinct elements there are
    frequency[k-1] += 1

plt.pie(frequency/10**5, labels=range(1,8),autopct='%1.1f%%')
plt.title('Number of distinct digits in a random phone number')
plt.show()
../_images/c648aeea43a54b43e160c2a6988d3c40836c5acbcc672252646dd6d72c1d378a.png
Contents