Lecture 7: Bayes’ Rule

STATS 60 / STATS 160 / PSYCH 10

---

Conditional Probability

Recall from last time that if we have two events, \(A\),\(B\), then “the probability of \(A\) conditioned on \(B\)” is just the probability that \(A\) happens, when we take into account that \(B\) has happened.

We write

\[\Pr[A \mid B]\]

---

How can we figure out \(\Pr[A \mid B]\)?

Example: A doctor orders a test for a patient to detect a rare disease. The test is 95% accurate. The disease affects 1% of the population.

The test comes back positive.

Question: How confident should the doctor be that the patient has the disease, given that the test came back positive?

For many people, their first impulse is to say the doctor should be 95% confident.

But as we will soon see, this is the common mistake of confusing \(\Pr[A \mid B]\) with \(\Pr[B \mid A]\).

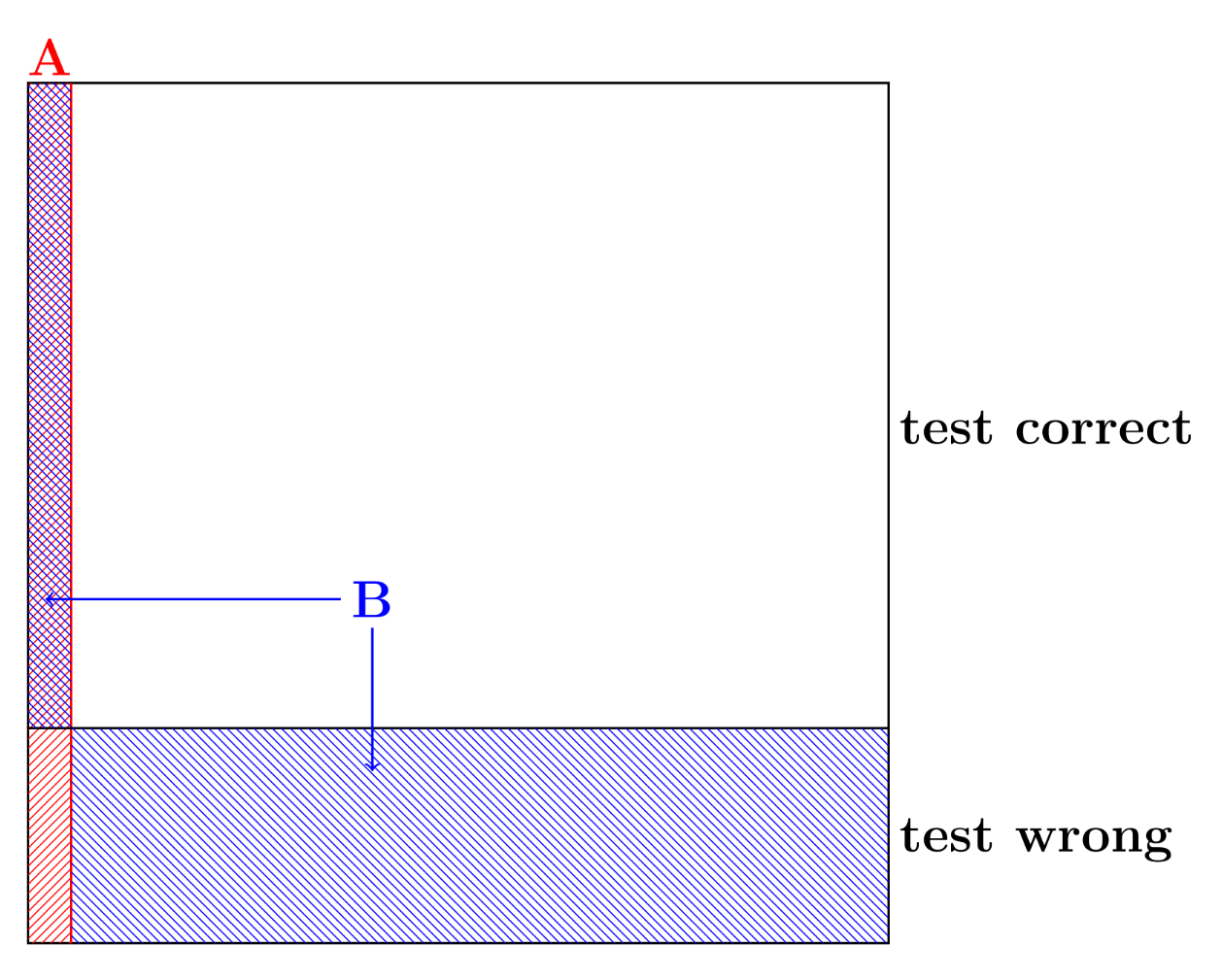
The blue-red region is true positives. The blue-only region is false positives.

---

Putting the scenario in the language of conditional probability

The blue-red region is true positives. The blue-only region is false positives.

Let \(A\) be the event that the patient has the rare disease.

Let \(B\) be the event that the test is positive.

The test is 95% accurate.

1. How can we express the accuracy of the test in the language of conditional probabilities?

2. How can we express our confidence that the patient has the disease, given that the test is positive, in the language of conditional probabilities?

3. How would you express \(\Pr[\overline{A} \mid B]\) in plain English?

We can express the test accuracy by saying that

\[\Pr[B \mid A] = 0.95 \quad \text{and} \quad \Pr[B \mid \overline{A}] = 0.05\]

This is a property of the test, determined previously in clinical trials.

Our confidence that the patient has the disease given that the test was positive is $\(\Pr[A \mid B].\)$

\(\Pr[\overline{A} \mid B]\) is the chance of a false positive.

---

Why is test accuracy not the same as confidence?

We know that the test is 95% accurate, in the sense that \(\Pr[B \mid A] = 0.95\).

But, taking the test accuracy for our confidence \(\Pr[A \mid B]\) ignores the fact that the disease is very rare, affecting only \(1\%\) of the population.

In the language of probability, \(\Pr[A] = 0.01\).

Consider the following picture:

The disease

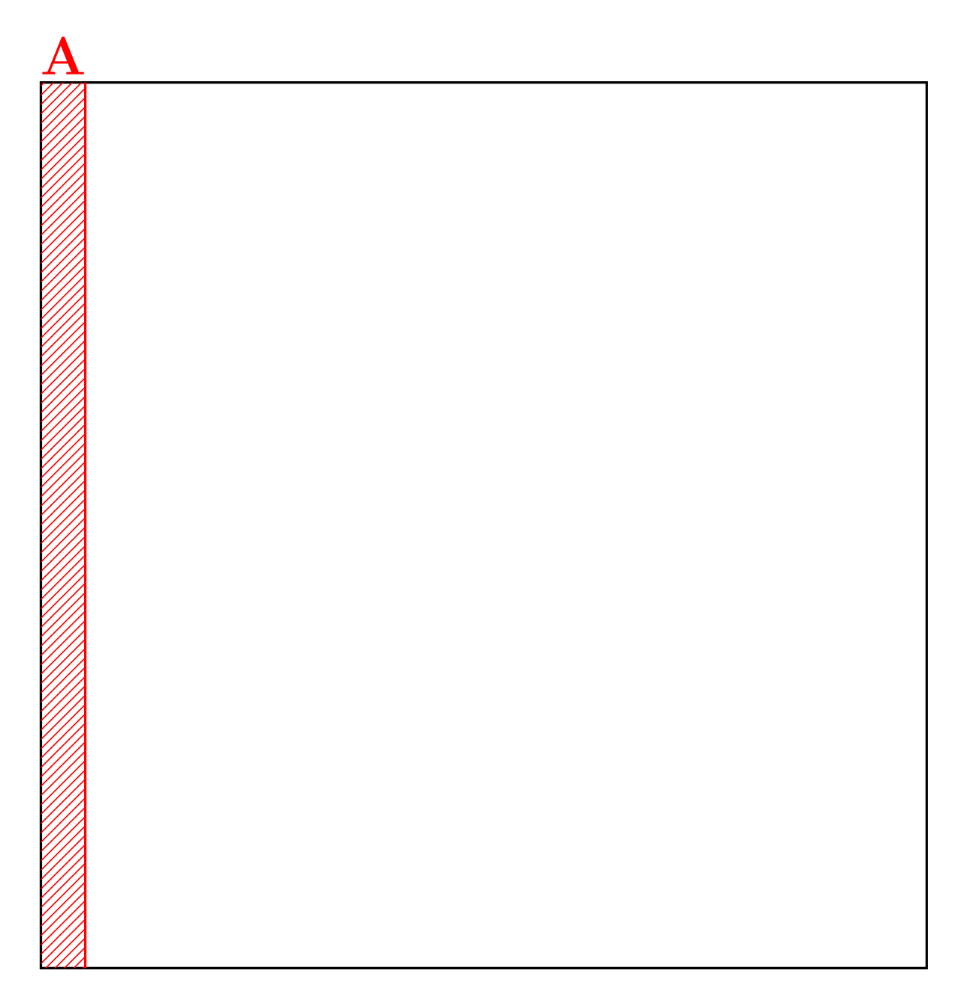
The red region represents the 0.01 fraction of people with the disease.

The test

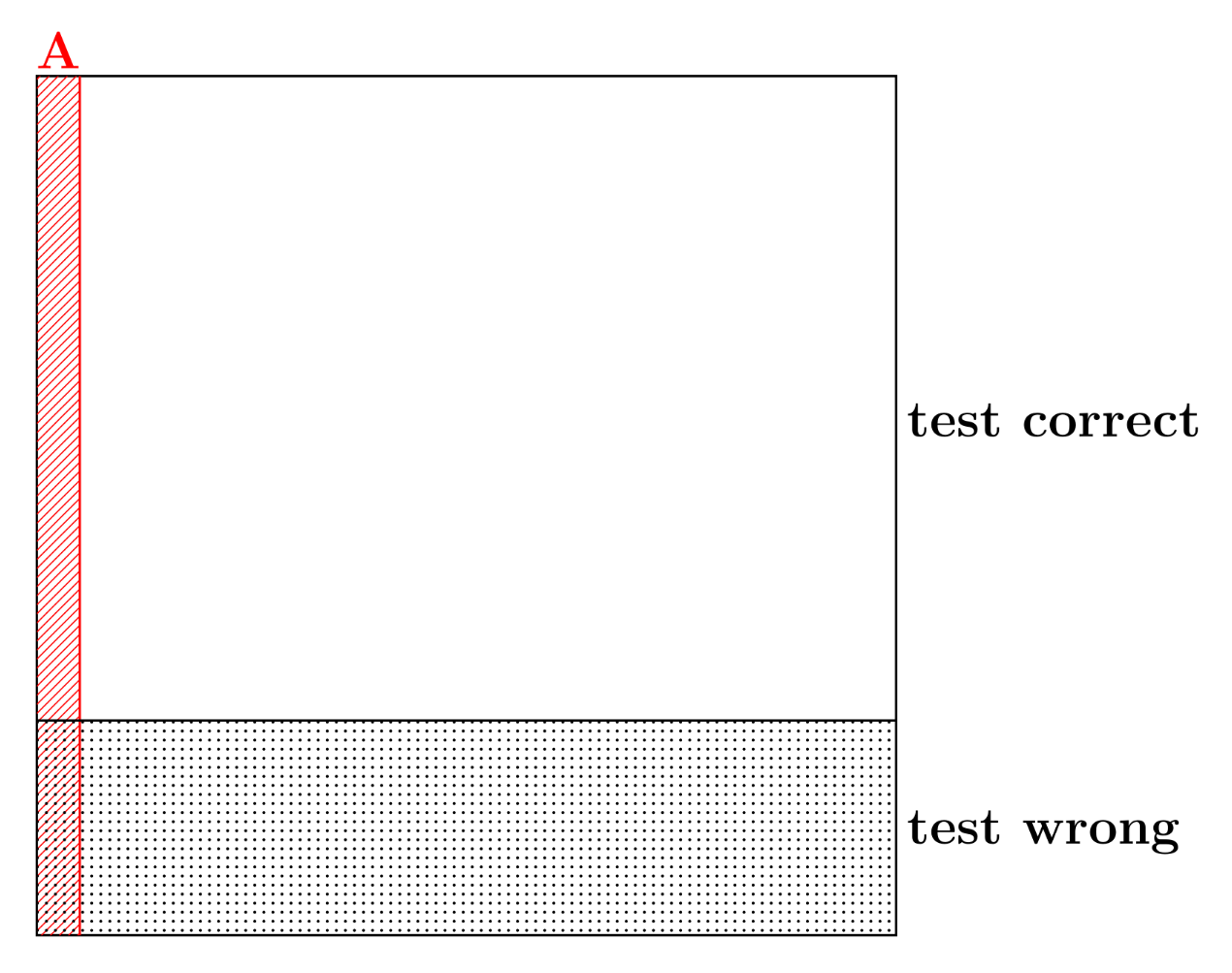
The dotted region represents the 0.05 fraction of time that the test is wrong.

The positive test

The blue region represents the event that the test is positive. The blue-red region is true positives. The blue-only region is false positives.

Even though the test is 95% accurate, the disease is so rare that most of the time when the test is positive (when \(B\) occurs), it is actually a false positive.

---

Bayes’ Rule

Bayes’ Rule is the following rule for computing conditional probabilities:

\[ \Pr[A \mid B] = \Pr[B \mid A] \cdot \frac{\Pr[A]}{\Pr[B]}. \]

So if we know the test accuracy, and we know how rare the disease is, we can decide how confident to be in the positive test result.

---

Computing the chance of a true positive

The disease affects \(1\%\) of the population, so \(\Pr[A] = 0.01\).

The test is \(95\%\) accurate, so \(\Pr[B \mid A] = 0.95\).

Bayes’ rule gives us that

\[ \Pr[A \mid B] = \Pr[B \mid A] \frac{\Pr[A]}{\Pr[B]} = 0.95 \cdot \frac{0.01}{\Pr[B]}. \]

Figuring out \(\Pr[B]\)

We can figure this out from the information we already have. We can use the law of total probability:

\[ \Pr[B] = \Pr[B \cap A] + \Pr[B \cap \overline{A}] \]

And then the definition of conditional probability:

\[ = \Pr[B\mid A]\cdot \Pr[A] + \Pr[B \mid \overline{A}] \cdot \Pr[\overline{A}] \]

And the law of complements:

\[ = \Pr[B\mid A]\cdot \Pr[A] + \Pr[B \mid \overline{A}] \cdot (1-\Pr[A]) \]

And finally, since the test is 95% accurate, \(\Pr[B \mid A] = 0.95\) and the probability of a false positive is \(\Pr[B \mid \overline{A}] = 0.05\), so we can plug in

\[ = 0.95\cdot 0.01 + 0.05 \cdot 0.99 = 0.059. \]

Final answer

Knowing that \(\Pr[B] = 0.059\), we return to Bayes’ rule, $\( \Pr[A \mid B] = \Pr[B \mid A] \cdot \frac{\Pr[A]}{\Pr[B]} = 0.95 \cdot \frac{0.01}{0.059} \approx 0.16. \)$

---

Takeaway #1: The base rate for the disease matters!

Because the disease is rare, even though the test is 95% accurate,

we can only be 16% confident that the patient actually has the disease!

The chance of a false positive is \(84\%\)!

---

Takeaway #2: Bayes’ rule

Bayes’ rule let us compute \(\Pr[A \mid B]\) from \(\Pr[B \mid A]\) without having to think hard about the sample space!

A second example: Steve

• This example is based on a lesson on Bayes Theorem by 3blue1brown.

• Steve is very shy and withdrawn, invariably helpful but with very little interest in people or in the world of reality. A polite and tidy soul, he has a need for order and structure, and a passion for detail.

• Is it more likely that Steve is a librarian or a farmer?

Baseline

There are roughly 20 times as many farmers as librarians

\[\mathrm{Pr}[\text{librarian}] = \frac{1}{21}\]

Updating

The description of Steve would match a higher proportion of librarians than farmers.

\[\mathrm{Pr}[\text{description} \mid \text{librarian}] = \frac{4}{10},\quad \mathrm{Pr}[\text{description}\mid \text{farmer}] = \frac{1}{10}\]

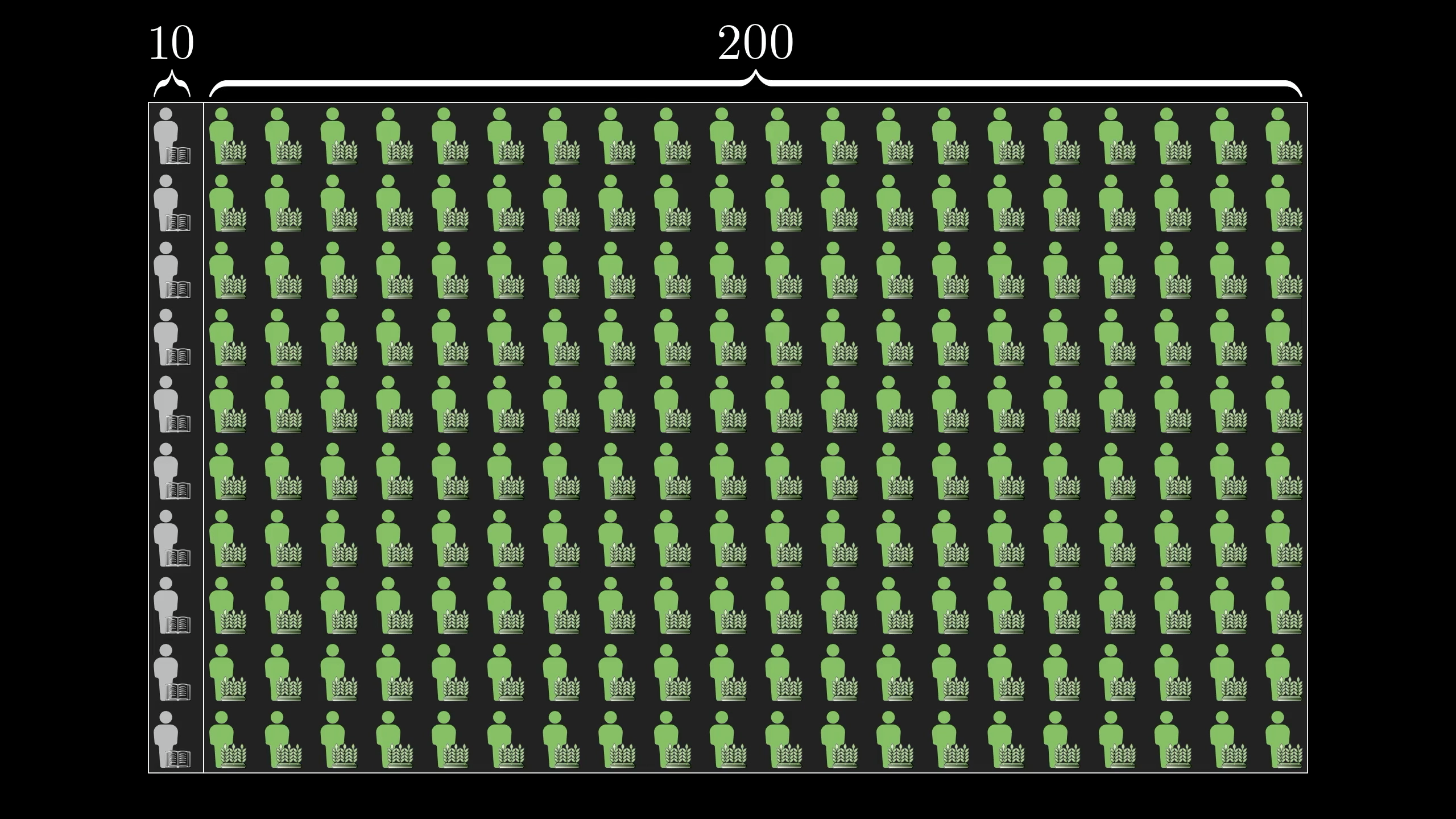
Question: how many librarians match the description? How many farmers match the description?

Bayes’ Rule

Bayes Rule

\[\Pr[\text{librarian} \mid \text{description}] = \frac{4}{24} = 16.7\% \]

Bayes’ Rule

\[\begin{align*} \Pr[\text{librarian} \mid \text{description}] &=\Pr[\text{description} \mid \text{librarian}] \frac{\Pr[\text{librarian}]}{\Pr[\text{description}]}\\ & = \frac{4}{10} \cdot \frac{\frac{1}{21}}{\frac{4}{10}\cdot \frac{1}{21} + \frac{1}{10} \cdot \frac{20}{21} } \\ &= \frac{4}{24} \end{align*}\]

Bayes Rule

\[\Pr[A \mid B] = \frac{\Pr[A]\Pr[A\mid B]}{\Pr[B]}= \frac{\Pr[A]\Pr[B \mid A]}{\Pr[A]\Pr[B \mid A]+\Pr[\overline{A}]\Pr[B \mid \overline{A}]}\]