Lecture 18: Selection Bias#
STATS 60 / STATS 160 / PSYCH 10
Concepts and Learning Goals:
tl;dr for sample mean estimation
Unbiased, independent samples are crucial for sample mean estimator to work well!
Selection bias is the collection of samples in a way that introduces bias
Effects of selection bias
Sources of selection bias
Recap for accuracy of the sample mean#
Suppose we want to estimate the mean value \(\mu\) of some random variable \(x\) in a population. Suppose \(x\) has standard deviation \(\sigma_x\) in the population.
We studied the accuracy of the sample mean, \(\hat\mu_n = \frac{x_1+x_2+\cdots+x_n}{n}\).
Here are the key takeaways:
The sample mean is a random quantity; the sample is random, so the sample mean is random. A different sample could lead to a different value of the sample mean.
If the samples are independent and uniform then
a. The expected value of the sample mean is the population mean, \(\mathbb{E}[\hat\mu_n] = \mu\)
b. The standard deviation of the sample mean is proportional to the population standard deviation \(\sigma_x\), but decreases with larger sample size \(n\): $\(\text{standard deviation of sample mean} = \frac{\sigma_x}{\sqrt{n}}\)$
c. The distribution of the sample mean \(\hat\mu_n\) is close to the Normal distribution when \(n\) is large enough, no matter what the population distribution was!
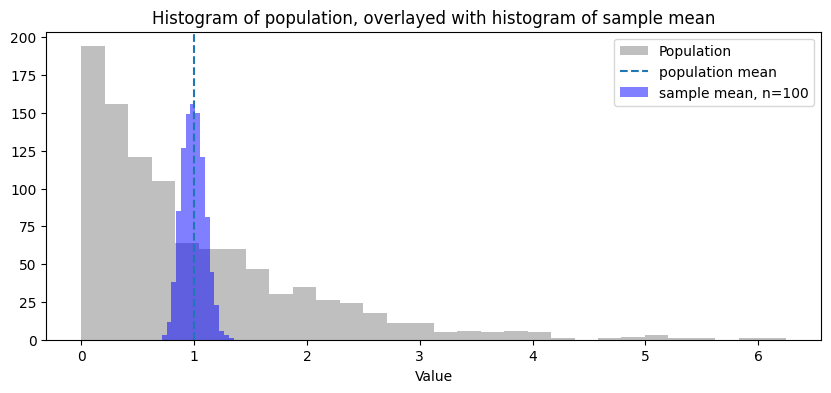
We often want to know how accurate \(\hat\mu_n\) is. Because the sample is random, we cannot exactly know what the error \(|\hat\mu_n - \mu|\) is.
But we can get confidence intervals which tell us how small the error is likely to be.
a. Think of this like a ring toss:
The population mean \(\mu\) is the post.
The \(68\%\), \(95\%\), and \(99\%\) confidence intervals around the sample mean \(\hat \mu_n\) are rings of progressively larger size. The same metaphor applies for a confidence interval of any confidence level.
The \(68\%\) confidence interval is large enough that it will land around the population mean \(68\%\) of the time.
Check out this video
b. Most of the time the sample mean will be within a few of standard deviations of the population mean: $\(|\hat\mu_n - \mu| \le C \frac{\sigma_x}{\sqrt{n}} \text{ for } C \le 3.\)$
The error decreases as the sample size increases!
Quantitatively: if you want error \(\approx \frac{1}{k}\), you need \(k^2\) samples.
To get 2x as accurate, you need 4x as many samples.
To get 10x as accurate, you need 100x as many samples.
c. When \(n\) is large enough, since \(\hat\mu_n\) is approximately Normal, we can use the \(68-95-99\%\) rule to get very precise confidence values:
\(68\%\) of the time, \(|\hat\mu_n - \mu| \le \frac{\sigma_x}{\sqrt{n}}\)
\(95\%\) of the time, \(|\hat\mu_n - \mu| \le 2\frac{\sigma_x}{\sqrt{n}}\)
\(99\%\) of the time, \(|\hat\mu_n - \mu| \le 3\frac{\sigma_x}{\sqrt{n}}\)
Unbiased samples are crucial#
The theory from the past two lectures applies to independent and uniform samples.
Independent: the fact that we collected sample \(x_i\) shouldn’t make it any more or less likely that we collect sample \(x_j\).
The most extreme case of non-independence is that we just take one sample \(x_1\) and then take \(n-1\) copies of it for \(x_2,\ldots,x_n\).
Independent samples are crucial to make sure that the variability of the sample mean decreases like you expect as the sample size grows.
Question: can you come up with a realistic example of a sampling method where samples might not be independent?
Uniform: we should be sampling uniformly from the population, not favoring any subsets over the other.
Question: Suppose you are trying to conduct a poll to figure out which candidate is likely to win the congressional race in your district. What are the challenges to collecting a uniform sample? Can you think of a way of doing it?
Luckily, the same theory basically applies if our samples are just independent and unbiased.
Unbiased: the population distribution of the samples has the same mean as the population mean.
It’s still hard to get unbiased samples!
When you sample in a way that introduces bias, this is called selection bias.
The Gettysburg Address#
Pick a random word from the Gettysburg Address, on the back of your worksheet.
Enter your word here:

Was our sample biased?#
Common sources of bias#
Sampling bias#
Sampling bias occurs when you disproportionately include or exclude a particular demographic from your sample.
Question: Can you think of other real-life examples of sampling bias?
Convenience sampling leads to sampling bias#
Convenience sampling: When studies are done on a convenient-to-reach population. The convenient population might not be representative of the whole.
Example: Experiments in the social sciences (psychology, behavioral economics) are disproportionately done on college students (because they are conducted by college professors).
One of many stories: In 1990 Khaneman, Knetsch, and Thaler, did the following experiment to test for “the endowment effect” (where people place a higher value on items they already own):
The participants were all Cornell undergrads.
They gave half the participants a coffee mug.
The participants who got the coffee mugs were asked to state a price they’d be willing to sell for. The participants who did not get coffee mugs were asked to state how much they’d be willing to buy for. This was implemented in multiple rounds in such a way that participants knew the market price for the mugs (where supply/demand curves meet).
There was a disparity between prices—on average sellers demanded almost twice as much as buyers were willing to pay.
Later, List, 2003 tried to replicate the study with a different population: people participating in a sportscard (e.g. baseball card) tradeshow, and participants participating in a collector pin trading show.
The same experiment in this population did not observe an endowment effect.
List hypothesizes that market experience might explain the endowment effect. The initial dramatic finding could be due to the use of a convenience sample of college students, who do not tend to have a lot of market experience due to their youth.
Method of contact leads to sampling bias#
The way that participants are recruited/contacted screens some people out, and selects for others.
Example: Election polling with landline phones. There are several famous incidents of this sort. Here is one:
In 2012, Gallup, Inc. predicted that Mitt Romney would win the 2012 presidential election.
Barak Obama ended up winning.
Incorrect predictions can happen to anyone, but the Gallup predictions were among the worst, in a quantitative sense, systematically over-predicting the success of Republicans.
Reviewing their performance, Gallup researchers identified phone-call based polling as a major source of bias.
Specifically, about half of the participants were reached by calling listed landline numbers; participants with a listed landline tend to skew older and more conservative.
Lack of access leads to sampling bias#
Some of the population is not accessible to you.
Example: hot guys are jerks (Lecture 8)
Volunteer bias#
Volunteer bias occurs when study participation is voluntary, and a biased subset of the population is more likely to volunteer.
Ratings/Customer experience#
People who had an extreme experience are more likely to rate and respond.
Some studies find that if you seek out additional reviewers (by offering incentives) then average rating drops.
Compensation#
Some studies offer participants compensation in order to convince them to participate.
Question: What kind of bias do you think this might introduce?
Surveys with compensation offered are likely to appeal to those who have more use for compensation.
Example: In the 2000’s and 2010’s, the Bureau of Labor Statistics was having trouble recruiting participants for the “Consumer Quarterly Expenditures Survey,” which aims to measure household expenses.
The Bureau conducted an experiment to check if offering incentives of a prepaid debit card (either for initial participation or on completion of the interview) would be an effective way of increasing participation.
Among those who agreed to participate, the mean and median income level, and the rate of home ownership, is lower in the group that got the prepaid debit card.
Question: Can you think of other real-life examples of volunteer bias?
Survivorship bias#
Survivorship bias is the phenomenon where bias is introduced by screening participants.
In clinical trials:
A famous example of a clinical trial where results were skewed by survivorship bias is High-dose chemotherapy and bone marrow transplant treatment for breast cancer in the 80’s and 90’s.
Only women who did not have a bad response to conventional chemotherapy were eligible for the early phases of the trial.
The early phases of the trial showed very favorable results.
Later phases of the trial showed that the therapy is not effective.
What went wrong? Conditioning on having responded well to conventional chemotherapy, you are more likely to survive on this alternative therapy.
Question: Can you think of other real-life examples of survivorship bias?
Recap#
A biased sample can make estimates inaccurate
Common sources of selection bias:
Sampling bias
Volunteer bias
Survivorship bias
